10. Факторный анализ
Факторный анализ — представляет собой метод обобщения или сокращения большого количества переменных, объединение их в группы на основе характерных связей. В факторном анализе переменные не делятся
на независимые и зависимые.
В практике маркетинговых исследований с факторный анализ применяется в следующих ситуациях
- для сегментирования рынка и выявления переменных с целью группировки потребителей;
- для определения характеристик торговой марки с целью выявления предпочтений потребителей;
- при разработке рекламной стратегии с целью выявления особенностей восприятия потребителем рекламного продукта
Факторный анализ применяется для выделения из большого массива данных малое число групп, состоящих из переменных, объединенных общими факторами (Рисунок 10.1).
Рисунок 10.1 –Диалоговое окно факторного анализа
В один фактор объединяются переменные, плотно коррелирующие между собой и слабо коррелирующие с переменными, которые объединяются на основе других факторов. Факторный анализ проводится с целью
сокращения числа переменных и упрощение процедуры анализа существующей базы данных.
В процессе проведения факторного анализа рассчитываются и анализируются следующие показатели:
- Критерий сферичности Бартлетта — показатель, с помощью которого проверяют, отличаются ли корреляции от 0. Если г близко к нулю, то выбранная переменная не взаимосвязана с другими.
Значимость меньше 0,05 указывает, на то что проведение факторного анализа приемлемо. - Корреляционная матрица — матрица, включающая в себя все возможные коэффициенты корреляций r между анализируемыми перемнными.
- КМО — мера адекватности выборки Кайзера—Мейера—Олкина — величина, используемая для оценки применимости факторного анализа. Значения от 0,5 до 1 говорят об адекватности факторного анализа,
значения до 0,5 указывают на то, что факторный анализ неприменим к выборке.
Графическое изображение критерия “каменистой осыпи” — график собственных значений факторов, расположенных в порядке убывания, используется для определения достаточного числа факторов.
Процедура факторного анализа включает следующие этапы:
- Формулировка проблемы.
- Проверка возможности проведения, вычисление корреляционной матрицы.
- Выбор метода факторного анализа.
- Извлечение факторов.
- Вращение факторов.
- Определение значений факторов.
- Проведение подгонки выбранной модели.
Пример. Проведем факторный анализ с целью сокращения массива данных, содержащих информацию о мотивах туристов, при выборе места отдыха за городом. Оптимизируем структуру данных, сократив
число переменных.
Основные задачи:
- оценить возможность проведения и адекватность факторного анализа для данной выборки;
- вычислить корреляционную матрицу и выявить взаимосвязи между переменными базы данных;
- выявить и извлечь необходимое количество факторов для создания упрощенной структуры;
- разбить базу данных на группы факторов на основе значений совместной корреляции;
- подобрать названия созданным переменным.
Вверх
Мотивы туристов, при выборе места отдыха за городом:
- близость к городу
- приемлемые цены
- близость водоема, леса
- уровень комфорта
- тишина, уединение
- хорошее питание
- наличие развлечений
- комфорт отдыха с детьми
- возможность лечения, ухода за здоровьем
Пошаговая инструкция
ШАГ 1. Меню “Анализ — Сокращение размерности — Факторный анализ …”. Открывается диалоговое окно “Факторный анализ”.
ШАГ 2. Из этого списка переменных выбрать необходимый массив, и перенести его в поле “Переменные”.
Если есть необходимость провести факторный анализ отдельно для двух переменных, например мужчин и женщин, то в поле “Переменная отбора наблюдений” вносится переменная “пол”. В данном
случае нет необходимости проводить такое деление.
ШАГ 3. Диалоговое окно “Описательные статистики— выбрать “КМО и критерий сферичности Бартлетта” для проведения тестов “КМО” и “Бартлетт”, проверяющих пригодность
данных для проведения факторного анализа.
ШАГ 4. Диалоговое окно “Описательные статистики— “Корреляционная матрица— “Коэффициенты— “Продолжить”.
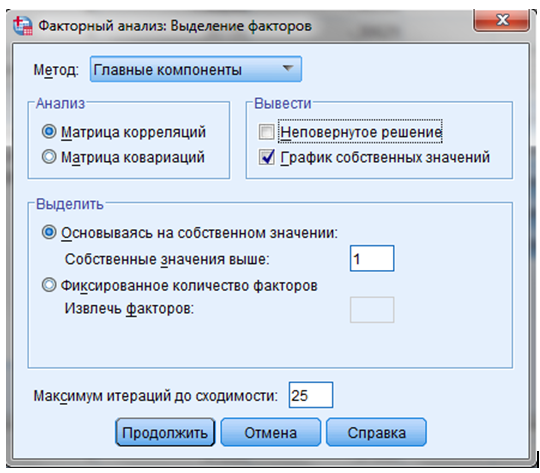
ШАГ 5. Диалоговое окно “Извлечение— задать условия определения количества факторов. В диалоговом окне “Извлечение— выбрать метод “Главные компоненты. — “Матрица корреляций”
(Рисунок 10.2).
Рисунок 10.2 — Матрица корреляций
ШАГ 6. Задать условие: собственное значение больше “1”. При данном условии программа определит факторы в количестве больше 1.
ШАГ 7. Вывести график собственных значений — “График собственных значений— “Продолжить”.
ШАГ 8. Выбор ротации матрицы коэффициентов: в главном диалоговом окне “Факторный анализ— диалоговое окно “Вращение— метод ротации “Варимакс— “Продолжить”.
ШАГ 9. Создание новых переменных: в диалоговом окне “Факторный анализ— диалоговое окно “Значения факторов— отметить команду “Сохранить как переменные— метод
расчета значений новых переменных “Регрессионная модель”. В итоге создаются новые переменные, которые можно будет использовать в дальнейшем анализе.
ШАГ 10. “ОК”.
Интерпретация результатов
- Величина КМО показывает приемлемую адекватность выборки для факторного анализа КМО = 0,512>0,5. Критерий Бартлетта (p<0,05), что говорит о целесообразности факторного анализа в
силу коррелированности факторов. - Выявление и извлечение необходимого количества факторов для создания упрощенной структуры
Компонента Начальные собственные значения Суммы квадратов нагрузок вращения Всего % дисперсии Кумулятивный % Всего % дисперсии Кумулятивный % 1 2,57 25,7 25,7 2,07 20,76 20,76 2 1,79 17,95 43,66 1,84 18,47 39,23 3 1,4 14,02 57,68 1,56 15,62 54,86 4 1,23 12,29 69,97 1,34 13,42 68,28 5 1,07 10,79 80,77 1,24 12,48 80,77 6 ,87 8,69 89,47 7 ,43 4,31 93,78 8 ,34 3,43 97,21 9 ,27 2,7 99,91 10 ,008 ,08 100,0 Метод выделения: Анализ главных компонент.
Начальные собственные значения должны быть больше 1.
Оптимальное число факторов — 5. Такая модель сохраняет 80,77% исходной информации, при этом число фактор сокращается в два раза.
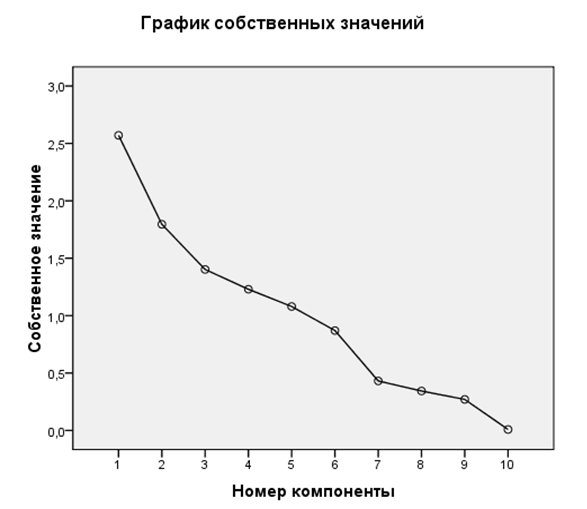
Рисунок 10.1 — График собственных значений
График показывает соответствующие собственные значения в системе координат: с 5 по 6 факторы происходит перелом графика. Это подтверждает, что оптимальное количество факторов 5.
- На основании ротированной матрицы (таблица 10.5) компонентов в одну группу собираются переменные, которые наиболее тесно взаимосвязанные между собой (наиболее высокое значение коэффициента корреляции). В результате программа группирует переменные исходного массива и создает матрицу преобразования компонент (таблица 10.6)
Компонента 1 2 3 4 5 близость к городу -,088 ,852 -,198 -,009 ,147 приемлемые цены ,278 -,190 -,221 -,561 ,622 близость водоема, леса ,074 -,240 -,210 ,664 ,215 уровень комфорта -,062 ,793 ,241 ,093 -,148 тишина, уединение ,988 -,074 ,082 -,040 -9,640E—6 хорошее питание ,059 ,331 ,831 ,158 ,054 наличие развлечений -,075 ,335 -,797 ,261 -,070 комфорт отдыха с детьми -,086 ,078 ,179 ,221 ,874 возможность лечения, ухода за здоровьем ,991 -,071 ,026 -,021 ,006 организация детского отдыха -,084 ,400 ,087 ,659 -,004 Таблица 10.5 — Матрица повернутых компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.Компонента 1 2 3 4 5 1 -,69 ,61 ,023 ,36 -,12 2 ,55 ,48 ,64 ,19 ,03 3 ,45 ,35 ,75 ,32 ,002 4 -,101 -,008 ,000 ,14 ,98 ,020 ,51 -,130 -,83 ,123 Таблица 10.6 — Матрица преобразования компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.Выделяем следующие факторы:
Фактор 1 — тишина и уединение, уход за здоровьем
Фактор 2 — близость к городу, уровень комфорта
Фактор 3 — хорошее питание, наличие развлечений
Фактор 4 — организация детского отдыха, близость водоем
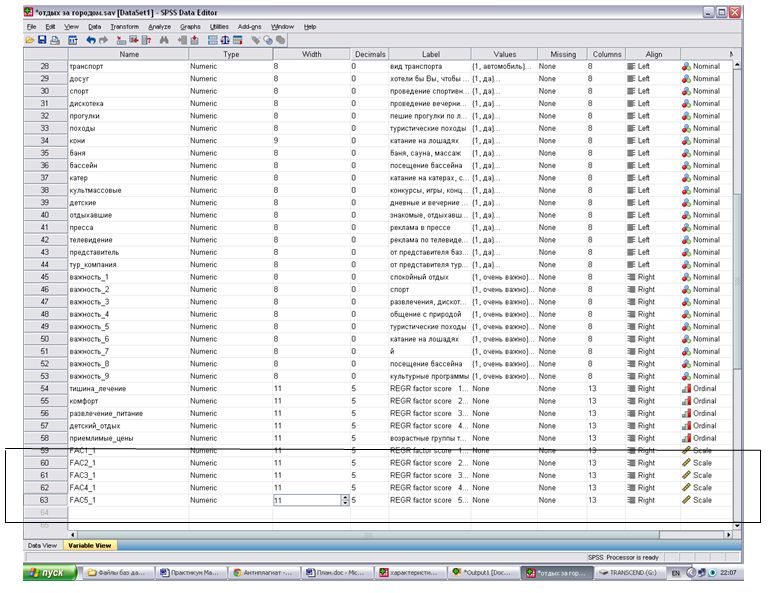
Фактор 5 — комфорт отдыха с детьми, приемлемые цен - В базе данных автоматически переносятся новые переменные построенной факторной модели (Рисунок 10.2). В столбце “Метка” отображается номер компонента факторной модели.
Рисунок 10.2 — Фрагмент вкладки “Переменные”
Названия новых компонент необходимо занести в исходную базу данных в столбец “Метка” таблицы “Переменные”, компьютер автоматически вычисляет значения новых переменных.
Суть новых переменных сводится к следующему: наибольшее отрицательное значение говорит о большей значимости переменной, и наоборот, наибольшее положительное значение говорит о наименьшей значимости переменной.
Созданные переменные в дальнейшем могут использоваться для анализа, например для проведения кластерного анализа.
| Мера адекватности и критерий Бартлетта | ||
|---|---|---|
| Мера выборочной адекватности Кайзера—Мейера—Олкина | ,512 | |
| Критерий сферичности Бартлетта | Приблиз. хи—квадрат | 262,3 |
| ст.св. | 45 | |
| Знч. | ,000 |
Таблица 10.1 — Результаты теста КМО и Бартлетта
| близость к городу | приемлемые цены | близость водоема, леса | уровень комфорта | тишина, уединение | хорошее питание | наличие развлечений | комфорт отдыха с детьми | возможность лечения, ухода за здоровьем | организация детск. отдыха | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Корреляция | близость к городу | 1,000 | -,060 | ,009 | ,519 | -,172 | ,149 | ,322 | ,075 | -,166 | ,241 |
| приемлемые цены | -,060 | 1,000 | -,064 | -,341 | ,270 | -,247 | -,121 | ,232 | ,273 | -,407 | |
| близость водоема, леса | ,009 | -,064 | 1,000 | -,056 | ,017 | -,083 | ,107 | ,114 | ,027 | ,030 | |
| уровень комфорта | ,519 | -,341 | -,056 | 1,000 | -,113 | ,384 | ,070 | ,008 | -,125 | ,256 | |
| тишина, уединение | -,172 | ,270 | ,017 | -,113 | 1,000 | ,084 | -,167 | -,060 | ,989 | -,129 | |
| хорошее питани | ,149 | -,247 | -,083 | ,384 | ,084 | 1,000 | -,422 | ,191 | ,036 | ,237 | |
| наличие развлечений | ,322 | -,121 | ,107 | ,070 | -,167 | -,422 | 1,000 | -,045 | -,116 | ,248 | |
| комфорт отдыха с детьми | ,075 | ,232 | ,114 | ,008 | -,060 | ,191 | -,045 | 1,000 | -,053 | ,202 | |
| возможность лечения, ухода за здоровьем | -,166 | ,273 | ,027 | -,125 | ,989 | ,036 | -,116 | -,053 | 1,000 | -,106 | |
| организация детск. отдыха | ,241 | -,407 | ,030 | ,256 | -,129 | ,237 | ,248 | ,202 | -,106 | 1,000 |
Таблица 10.2 — Корреляционная матрица.
Коэффициенты корреляции характеризуют плотность связи между переменными исходного массива.
Для того, чтобы рассчитать факторный анализ используя статистически пакет SPSS необходимо сделать следующий шаги:
1. Внести значения переменных по которым необходимо рассчитать факторный анализ. Данные вносятся в таблицу Data Editor. (Например 8 переменных var1…var8)
2. Выбираем Analyze -> Data reduction -> Factor…
3. В появившемся окошке под переносим нужные нам переменные из правой части в левую (var1…var8)
4. нажимаем кнопку Extraction…
4.1. В появившемся окне выбираем Principial components.
4.2. Отмечаем галочкой Scree plot
4.3. Нажимаем Continue
5. Затем нажимаем кнопку Rotation.
5.1. В поле Method из выпадающего списка выбираем Varimax
5.2. Нажимаем кнопку Continue
6юНажимаем кнопку Options
6.1. В поле Coefficient display format отмечаем галочкой Suppress absolute values less then 0,1
6.2. Нажимаем кнопку Continue
7. Смотрим результаты
19.1. Порядок выполнения факторного анализа
На первом шаге процедуры факторного анализа происходит стандартизация заданных значений переменных (z-преобразование);
затем при помощи стандартизированных значений рассчитывают корреляционные коэффициенты Пирсона между рассматриваемыми переменными.
Исходным элементом для дальнейших расчётов является корреляционная матрица. Для понимания отдельных шагов этих расчётов потребуются хорошие знания, прежде всего, в области операций над матрицами.
Для построенной корреляционной матрицы определяются, так называемые, собственные значения и соответствующие им собственные векторы, для определения которых используются оценочные значения
диагональных элементов матрицы (так называемые относительные дисперсии простых факторов).
Собственные значения сортируются в порядке убывания, для чего обычно отбирается столько факторов, сколько имеется собственных значений, превосходящих по величине единицу.
Собственные векторы, соответствующие этим собственным значениям, образуют факторы; элементы собственных векторов получили название факторной нагрузки.
Их можно понимать как коэффициенты корреляции между соответствующими переменными и факторами. Для решения такой задачи определения факторов были разработаны многочисленные методы,
наиболее часто употребляемым из которых является метод определения главных факторов (компонентов).
Описанные выше шаги расчёта ещё не дают однозначного решения задачи определения факторов. Основываясь на геометрическом представлении рассматриваемой задачи,
поиск однозначного решения называют задачей вращения факторов. И здесь имеется большое количество методов, наиболее часто употребляемым из которых является
ортогональное вращение по так называемому методу варимакса. Факторные нагрузки повёрнутой матрицы могут рассматриваться как результат выполнения процедуры факторного анализа.
Кроме того на основании значений этих нагрузок необходимо попытаться дать толкование отдельным факторам.
Если факторы найдены и истолкованы, то на последнем шаге факторного анализа, отдельным наблюдениям можно присвоить значения этих факторов, так называемые факторные значения.
Таким образом для каждого наблюдения значения большого количества переменных можно перевести в значения небольшого количества факторов.
Факторный анализ — это статистический инструмент, довольно часто используемый в психологии при создании многофакторных тестов, а также при систематизации и обобщении комплексных наблюдений.
Многочисленные варианты его использования включают конструирование тестов, выявление основных параметров личности и способностей, установление того, сколько отдельных психологических характеристик
(т.е. черт) измеряется набором тестов или заданиями теста.
Термин «факторный анализ» может относиться к двум довольно разным статистическим методикам:
-
Исследовательский факторный анализ (эксплораторный факторный анализ) — более старая и более простая методика.
-
Конфирматорный факторный анализ и его разновидности (известные как «анализ путей», «анализ латентных переменных» или «модели LJSREL») полезны во многих областях
за пределами изучения индивидуальных различий и особенно популярны в социальной психологии. Авторы не всегда четко указывают, какой из видов факторного анализа использовался —
исследовательский или конфирматорный. Если вы увидите термин «факторный анализ» в журнале, следует допустить, что имеется и виду исследовательский факторный анализ.
Часто при создании психологического теста важно, чтобы все задания шкалы измеряли одну (и только одну) психологическую переменную.
Коэффициент альфа Кронбаха может служить показателем надежности шкалы. Эта техника исходит из того,
что все задания в тесте формируют одну шкалу и коэффициент надежности, в сущности, проверяет, насколько это допущение обоснованно.
Однако рассмотрим более простой пример. В интересах науки планируете собрать следующие данные у случайно сформированной выборки, например, у 200 студентов:
• V 1 — вес тела (в кг);
• V 2 — степень невнятности речи (ранжируется по шкале от 1 до 5);
• V 3 — длина ноги (в см);
• V 4 — разговорчивость (ранжируется по шкале от 1 до 5);
• V 5 — длина руки (в см);
• V 6 — степень шатания при попытках пройти по прямой линии (ранжируется по шкале от 1 до 5).
Кажется вероятным, что V1 ,V3 и V5 будут варьировать совместно, поскольку крупные люди будут склонны иметь длинные руки и ноги и больше весить. Все эти три пункта измеряют некоторое
фундаментальное свойство индивидуумов вашей выборки: их размеры. Точно так же вероятно, что V2, V4 и V6 будут варьировать совместно, так как количество употребленного алкоголя,
вероятно, будет связано с четкостью речи, разговорчивостью и с осложнениями при попытках пройти по прямой линии. Таким образом, хотя мы собрали шесть фрагментарных данных,
эти переменные измеряют только 2 конструкта: размеры тела и степень опьянения. В факторном анализе вместо слова «конструкт» обычно используется слово «фактор», и далее мы будем следовать этой традиции.
Исследовательский факторный анализ, по существу, выполняет две функции:
-
Он показывает, сколько отдельных психологических конструктов (факторов) измеряется данным набором переменных. В приведенном выше примере такими двумя факторами являются размеры тела и степень опьянения.
-
Он показывает, какие именно конструкты измеряют использованные переменные. В приведенном выше примере было показано, что VI , V 3 и V 5 измеряют один фактор и V2, V4 и V6 измеряют другой, совершенно отличный фактор.
В некоторых формах факторного анализа дополнительно можно прокоррелировать факторы между собой, и затем вычислить для каждого испытуемого индивидуальную оценку по каждому фактору в целом («факторные оценки»).
Оценки по полным тестам (а не по его отдельным заданиям) также могут подвергаться факторному анализу — на самом деле именно так эта методика и используется. Факторный анализ в этом случае может показать, действительно ли тесты, которые, предположительно, измеряют один и тот же конструкт (например, шесть тестов, которые претендуют на измерение тревожности), продуцируют один фактор, или же в этом случае будут выделены несколько факторов (указывая на то, что тесты на самом деле измеряют несколько разных характеристик). Факторный анализ оценок, полученных на основе полных тестов, может быть чрезвычайно полезен для установления того, что именно измеряется группой тестов, поскольку многозначность языка допускает, что одному и тому же конструкту разными исследователями могут быть даны различные наименования. «Тревога» у одного автора может обозначать то же самое, что «нейротизм» — у другого или «негативный аффект» — у третьего. Число терминов, используемых в психологии индивидуальных различий, потенциально безгранично, и без факторного анализа нет надежного способа установить, действительно ли несколько шкал измеряют один и тот же базисный психологический феномен. Например, если в издательском каталоге указано, что имеются психологические средства измерения «нейротизма», «тревоги», «истерии», «силы Эго», «нервозности», «низкой самоактуализации» и «боязливости», кажется разумным задать вопрос: действительно ли это шесть отдельных понятий или это одна и та же характеристика, которой исследователи, имеющие разные теоретические воззрения, дали различные названия? Факторный анализ может точно ответить на этот вопрос, и поэтому он чрезвычайно полезен для упрощения структуры личности и способностей.
Возможности факторного анализа не ограничиваются анализом заданий или оценок теста. Можно факторизовать, например, показатели времени реакции, взятые из когнитивных тестов различного типа, чтобы определить, какие из них (если такие есть) связаны между собой. Возможен и иной подход. Предположим, что группу школьников, которые не имели специальной спортивной подготовки или спортивной практики, оценивали с точки зрения их успешности в соревнованиях по 30 видам спорта с помощью комплекса оценок, включавшего рейтинги тренеров, регистрацию времени, среднюю длину броска, процент отсутствия очков при игре в крикет, забитые голы и любые другие измерения показателей успешности, наиболее подходящие для каждого вида спорта. Единственное условие состоит в том, что каждый ребенок должен участвовать в каждом виде соревнования. Факторный анализ обнаружит много интересных фактов; например, он покажет, будут ли индивидуумы, успешные в одной игре с мячом, демонстрировать тенденцию к успешности во всех остальных играх, будут ли соревнования по бегу на длинные и короткие дистанции образовывать две различные группы (и какой вид соревнования будет входить в какую группу) и т.д. Таким образом, вместо того чтобы обсуждать происходящее в терминах успешности в 30 различных областях, будет возможно суммировать эту информацию, обсуждая ее в категориях шести основных спортивных способностей (или стольких способностей, сколько выявит факторный анализ).
-
Принятие решения о качестве факторной структуры
Формальное
требование к факторной структуре
называется принципом простой структуры.
Это выражается в том, что каждая переменная
имеет близкие к нулю нагрузки по всем
факторам, кроме одного.
В настоящее время
не существует формальных критериев
простоты факторной структуры. Основным
критерием является возможность
содержательной интерпретации фактора
по двум и более исходным переменным.
Разработаны подходы
приближения к простой структуре путем
пошагового сокращения факторов и
переменных.
-
Если выявлен
фактор, по которому ни одна из переменных
не получила существенно большей (по
сравнению с другими факторами) нагрузки,
то стоит уменьшить число факторов. -
Если
фактор идентифицируется только по
одной переменной. А остальные не вошли
в него даже с второстепенными нагрузками,
то стоит уменьшить число факторов. -
Если имеются
неоднозначные переменные, то есть
переменные, которые имеют примерно
одинаковые по модулю факторные нагрузки
по двум и более факторам, то эти переменные
следует поочередно удалять из
исследования.
-
Вычисление оценок факторов
Оценки
факторных нагрузок являются коэффициентами
линейного уравнения, связывающего
значения факторов и значения исходных
переменных. Они показывают, с каким
весом входят исходные значения каждой
переменной в оценку факторов. Факторные
коэффициенты можно использовать для
вычисления факторных оценок для новых
объектов, не включенных ранее в факторный
анализ.
Факторные оценки
– значения факторов для конкретного
объекта. Факторные оценки отражают
структуру взаимосвязей исходных
признаков
-
Задачи, решаемые с использованием факторного анализа
С появлением
специализированных пакетов статистической
обработки информации появилась
возможность широкого применения
факторного анализа при решении
исследовательских и практических задач:
1.
Факторный анализ позволяет выделять
группы взаимосвязанных переменных.
2.
Факторный анализ позволяет сократить
исходное множество признаков до
нескольких факторов, которые отражают
разные стороны исследуемого объекта.
3.
Факторный анализ позволяет оценивать
количественно комплексные характеристики
объектов, учитывая реальную структуру
и взаимосвязь исходных переменных,
избегая потерь информации и оценивания
путем простого суммирования.
4.
Результаты факторного анализа могут
быть использованы для последующего
регрессионного, дискриминантного и
кластерного анализа.
-
Факторный анализ в spss
14.1. Вызов процедуры
Вызов процедуры
осуществляется командами Analyze/
Data
Reduction/
Factor…(рис.14-1)
Рис.14-1. Вызов
процедуры факторного анализа
Установка параметров
метода главных компонент производится
в нескольких диалоговых окнах. После
вызова процедуры откроется соответствующее
меню (рис.14-2). В диалоговом окне имеется
несколько кнопок, нажатие каждой из
которых открывает свое диалоговое окно.
Рис.14-2.
Вид окна
Factor Analysis
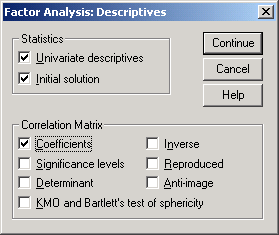
Рис.14-3.
Вид окна
Factor Analysis: Descriptives
В окне Factor
Analysis: Descriptives
имеются следующие возможности:
-
Univariate
descriptives
определение количества значащих
наблюдений, математическое ожидание
и стандартное отклонение по каждой
исходной переменной. -
Initial
solution
отображение исходных общностей
Communalities и процента
объясненной дисперсии. Для каждой
переменной общность
это доля дисперсии данной переменной,
которая может быть объяснена факторами
(компонентами). Естественно, изначально
доля объясненной дисперсии переменной
тождественно равна единице, поскольку
факторы-компоненты тождественно равны
переменным. В рассмотренном ниже случае
SPSS выделил две компоненты,
поэтому оценки общностей в следующем
столбце сообщают долю дисперсии
переменной, объясненной этими двумя
факторами. -
Coefficients
получение матрицы корреляции между
исходными переменными Х1 … ХК.
Метод
главных компонент предполагает анализ
матрицы корреляции Correlation matrix между Х1
… ХК. Те переменные, которые имеют
высокую степень корреляции, будут
объединены в компоненты.
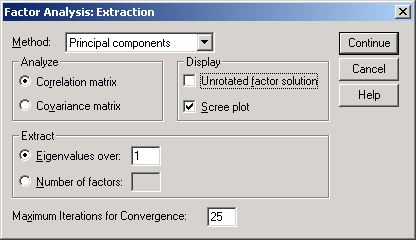
Рис.14-4. Вид окна
Extraction
Scree plot
график типа «осыпь» с собственными
значениями переменных по оси ординат
и их порядковыми номерами по оси абсцисс.
График можно использовать для выбора
числа факторов или порогового собственного
значения, поскольку он наглядно отражает
различие между большими и маленькими
собственными значениями (рис.14.5).

По умолчанию, SPSS
отбирает компоненты с собственными
значениями Eigenvalue, превосходящими 1.
Можно самостоятельно задать пороговое
значение или количество компонент (вне
зависимости от собственных значений).
Опция Rotation (Окно
Factor Analysis:
Rotation ) применяется с тем,
чтобы полученные результаты было легче
интерпретировать. SPSS осуществляет
вращение векторов так, чтобы каждой
исходной переменной соответствовало
наименьшее количество компонент. В SPSS
реализовано несколько методов вращения.
Например, Varimax метод
ортогонального вращения, который
облегчает интерпретацию компонент.
Рис.14-6.
Вид окна
Rotation
Loading plot (Окно Loading
Plot) график компонент
в повернутом пространстве. Координатами
точек этого графика являются нагрузки
трех первых компонент. Чем ближе
какая-либо координата к нулю, тем слабее
переменная ассоциируется с данной
компонентой (рис.14-7).

В
диалоговом окне Factor
Analysis:
Scores (рис. 14.8)
можно установить опцию о том, чтобы
выделенные компоненты были вычислены
и сохранены как новые переменные. После
проведения анализа методом главных
компонент, на них можно построить
регрессию. Обратим внимание – для
дальнейшего проведения процедуры
регрессия на главных факторах, необходимо
поставить флажок Display
factor Score
coefficient
matrix.
Рис.6-8.
Вид диалогового
окна Factor Analysis:
Scores
14.2.
Вид результатов расчета главных компонент
Результаты расчета
главных компонент представлены в
нескольких таблицах. Прокомментируем
некоторые из них.
6.2.4.1. Корреляционная
матрица (рис.6-9)
Рис.6-9. Вид
корреляционной матрицы
Корреляционная
матрица (рис.6-9) выглядит традиционно:
на пересечении строки и столбца находится
значение коэффициента корреляции между
этими переменными. По значению и знаку
судят о степени и направлению влияния
одной переменной на другую.
6.2.4.2. Таблица
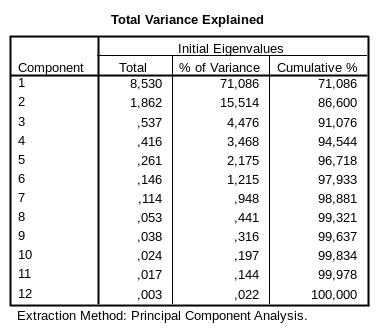
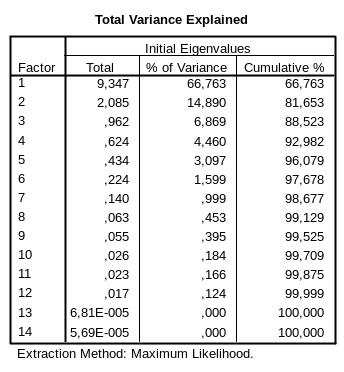
Total Variance Explained (рис.6-10)
В
этой таблице приводятся проценты общей
вариации, объясняемой каждым фактором.
Так 1- фактор объясняет 71,086% вариации;
2-й из оставшихся 28,914% объясняет 15,514%
(итого вместе два первых фактора объясняют
86,6%).
Рис.6-10.
Вид таблицы
Total Variance Explained
В
зависимости от предъявляемой пользователем
точности расчетов, из этой таблицы
выбирается число факторов, которые
необходимо учесть при дальнейших
расчетах.
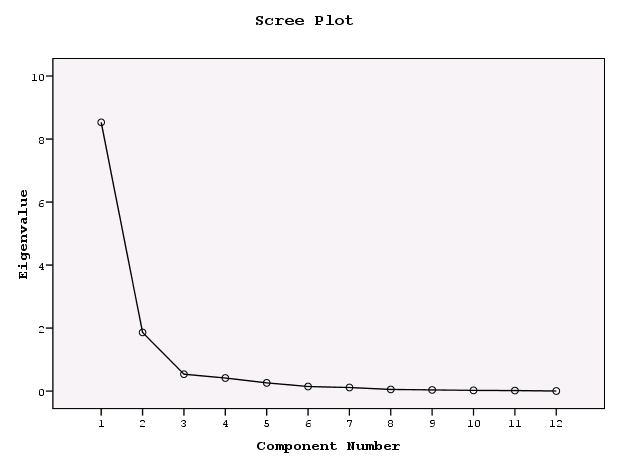
6.2.4.3. График Scree
Plot (рис.6-11)
Рис.6-11. График
процентов вариации, объясняемой каждым
фактором
График Scree
Plot представляет
собой графическое изображение таблицы
Total Variance
Explained.
6.2.4.4 Таблица
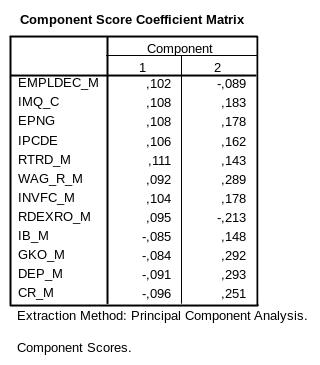
Score Coefficient Matrix (рис.6-12)
Результаты
этой таблицы могут понадобиться при
дальнейших расчетах регрессии на главных
факторах. В ней приводятся нагрузки
каждой переменной в нескольких главных
факторах. Так, в 1-ом факторе переменная
EMPLDEC имеет вес 0,102; переменная
IMQ – вес 0,108 и т.д.
Рис.6-12.
Таблица весов переменных в 2-х первых
факторах
6.2.4.5. Таблица
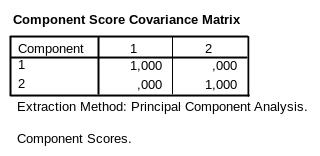
Component Score Covariance Matrix (рис.6-13)
В
таблице приведена степень влияния между
новыми переменными (главными факторами).
Обратите внимание, что компоненты
выбираются из условия, что они линейно
независимы и отражают максимально
возможную дисперсию, содержащуюся в
исходных данных.
Рис.6-13.
Независимость компонент друг от друга
6.3.
Факторный анализ. Метод максимального
правдоподобия с косоугольным вращением
6.3.1.
Вызов процедуры
Вызов процедуры
осуществляется командами:
Analyze
Data
Reduction
Factor…(рис.6-1).
6.3.2.
Установка параметров
В диалоговом окне
Factor Analysis
(рис.6-2) чтобы использовать
те же исходные данные щёлкните
на Reset, чтобы
восстановить значения по умолчанию, и
выберите в области Variables
переменные.
В окне Factor
Analysis:
Descriptives
можно оставить предыдущие параметры.
Рис.6-14.
Установка метода максимального
правдоподобия
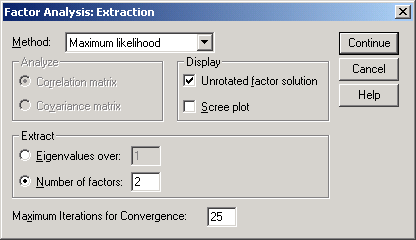
В окне Factor
Analysis:
Extraction
(рис.6-14) в поле
Method
установите
Maximum
likelihood
(метод максимального правдоподобия).
В области Extract
активизируйте Number
of factors:
2 (два фактора)…
Рис.6-15.
Установка параметров в окне Factor
Analysis:
Rotation
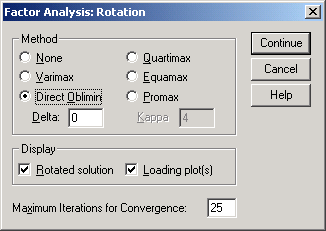
В окне Factor
Analysis: Rotation (Вращение) в области
Method активизируйте Direct
oblimin (рис.6-15).
В области
Display
активизируйте (рис.6-15)
Loading plot(s)
и Rotated solution.
В
окне Factor
Analysis: Factor Scores (рис.6-16)
активизируйте
Save as variables
(Сохранить как
переменные).
В
окне Factor
Analysis: Options (рис.6-17)
в области
Coefficient Display Format
активизируйте кнопки
Sorted by size
и
Suppress absolute values less
than: 0,20.
6.3.3.
Результаты расчета
Результаты
факторного анализа представлены в виде
таблиц общностей (рис.6-18) и объясненной
дисперсии (рис.6-19).
Рис.6-18.
Таблица общностей
Рис.6-19.
Таблица объясненной дисперсии
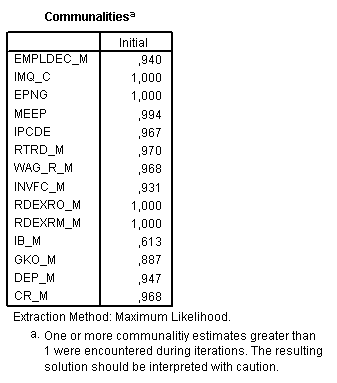
6.3.3.1. Таблица общности
Общности
(рис.6-18) выводятся до выделения факторов.
Для каждого метода выделения, за
исключением метода главных компонент,
оценка, размещающаяся в столбце Initial
(Начальная), равняется множественному
R-квадрат (коэффициенту
детерминации) с переменной текущей
строки в качестве зависимой и всеми
остальными в качестве независимых
переменных. Начальные общности
используются в вычислениях при выделении
факторов.
По
умолчанию, даже при использовании метода
максимального правдоподобия, для
определения числа факторов используется
метод главных компонент. Чтобы иметь
возможность сравнить полученные
результаты в методе максимального
правдоподобия с результатами из примера
1, мы в качестве параметра установили
выделение двух факторов (рис.6-14).
Общность
для переменной IBM
мала, так что она имеет слабое отношение
к обоим факторам.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Этапы факторного анализа
Учебный центр по изучению иностранного языка в Китае провел анкетирование по мотивации изучения китайского языка для иностранных студентов, обучающихся в центре. Используйте пятиуровневую шкалу Лайкерта. Первый уровень — наименее любимый, а пятый уровень — самый любимый. 18 человек были случайно выбраны для участия в опросе. Один из проектов исследовал «внутреннюю мотивацию» или «внутреннюю мотивацию интереса», чтобы понять приветствие и любовь иностранных студентов к китайскому языку и культуре. Проект разделен на шесть вопросов.
Организовать данные следующим образом
Сначала установите набор данных в spss
II.Главный диалог Open Factor analysis
1. Анализировать—Коэффициент уменьшения Deta
2. Поместите все данные в поле переменной
3. Войдите в поддиалог справа от главного диалога Факторного анализа.
(1) Описательный поддиалог
1. Выберите Univariables (статистику однофакторного описания): будут выведены среднее, стандартное отклонение и наблюдение для каждой переменной.
2. Выберите Начальное решение: будут выведены исходные результаты анализа: дисперсия общего фактора, ковариация, характеристические значения каждого фактора, процент от общей дисперсии и совокупный процент. Это система по умолчанию и должна быть сохранена.
3. Матрица корреляции (корреляционная матрица) ограждения, варианты включают выбираемые связанные индикаторы и соответствующие тесты:Часто выбирают (1) (4)
(1) Coeffieient (коэффициент корреляции), перечисляет матрицу коэффициентов корреляции между каждой переменной.
(2) Уровень значимости (уровень значимости), перечислите значение P для каждой переменной одностороннего теста.
(3) Определяющий (определитель) вариант, вывести определитель матрицы коэффициента корреляции.
(4)KMO and Barlett’s тесты сферичности (K-Kaiser, M-Meyer, O-Olkin): перечисляет результаты тестов сферичности и показывает, является ли факторная модель разумной.
(5) Обратный (обратная матрица): перечислить обратную матрицу коэффициентов корреляции.
(6) Воспроизведено (живая корреляционная матрица), перечислены оценочная корреляционная матрица и остаточный коэффициент после факторного анализа.
(7) Анти (обратное изображение): список отрицательной матрицы дисперсии изображения, включая отрицательное значение коэффициента корреляции, включая отрицательное значение дисперсии.
(2) Поддиалоговое окно извлечения.
1. Метод: семь методов не очень отличаются.Используйте основные компоненты по умолчанию (анализ основных компонентов):Начиная с вариации объясняющей переменной, дисперсию вариации можно объяснить главным компонентом, который в основном используется для получения результата начального фактора.
2. Aзализать забор:
(1) Корреляционная матрица (корреляционная матрица между переменными). Сохранить по умолчанию.
(2) Ковариационная матрица (ковариационная матрица между переменными)
3. Показать забор (выходной результат)
(1) А. Необращенное факторное решение (отобразить результат извлечения фактора без изменения вращения)
(2) График осыпания: горизонтальная ось — это число факторов, а вертикальная ось — это размер характеристического значения. График упорядочивает факторы в соответствии с размером характерных значений, и можно увидеть, какие из них являются основными. Максимум итераций для сходимости
4. Извлечь (установить коэффициент извлечения общего фактора) ограждения:
(1) Собственные значения превышены (в качестве критериев извлечения взяты характеристики, превышающие значения Mo).Оставьте значение по умолчанию для системы выбора по умолчанию 1.
(2) Количество факторов (количество самораспаковывающихся факторов).Оставьте значение выбора по умолчанию 1.
(3) Максимальные итерации для конвергенции, оставьте выбор по умолчанию 25.
4. Вращение
(1)method. Выберите Varimatrix (метод ортогонального вращения)
(2) Дисплей (вывод результатов)
Повернутое решение: Поверните ортогонально и выведите повернутую матрицу мод и матрицу преобразования коэффициентов.
б) график загрузки (график рассеяния нагрузки: трехмерный график: значение координаты является значением фактора, и каждая переменная распределена по трем точкам, что позволяет интуитивно понять взаимосвязь между переменной и фактором.
5. Баллы (коэффициент фактора).Сохранить по умолчанию。
6. Опции, оставьте настройки по умолчанию.Сохранить по умолчанию。
Описание формыСообщества (Таблица отклонений общего фактора): Таблица показывает долю информации в каждой предложенной переменной. Самый высокий уровень извлечения — китайские песни 0,874, а самый низкий уровень — китайская драма 0,652.
Диаграмма показывает, что Total Variance Explained (переменная пропорциональная таблица объяснений), также известная как список основных компонентов, является очень важной таблицей. Чем выше доля дисперсии, объясняемой фактором, тем больше этот фактор содержит исходную переменную информацию. Начальное значение признака первого компонента составляет 2,231, коэффициент объяснимой дисперсии составляет 31,621%, а второй и третий — 25,6% и 21,4% соответственно. Все остальные четыре компонента меньше 1, что указывает на то, что объяснительная сила этих компонентов не так велика, как исходная переменная, введенная напрямую. Эти семь переменных нужно только извлечь первые три компонента, а именноМожет.
Пояснение к диаграмме: На гравийной карте Scree Plot собственные значения начиная с третьего компонента очень низкие. Третий компонент — это «точка перегиба» этой фигуры. До этого является основным фактором, после этого является вторичным фактором. Таким образом, эта гравийная карта интуитивно показывает нам, что в нашем примере нужно извлечь только три основных компонента.
Описание диаграммы: Component Matrix В таблице матрицы компонентов указана доля каждой переменной, которая может быть объяснена фактором, когда метод ротации не используется (сколько информации о каждой переменной извлекает основной компонент).
Описание диаграммы: В таблице указана доля каждой переменной, которую фактор может объяснить после использования метода ротации. Из таблицы 5 видно, что после поворота исходное большее соотношение становится больше, а меньшее — меньше.
Extraction Method: Principal Component Analysis: Метод извлечения: анализ главных компонентов
Rotation Method: Varimax with Kaiser Normalization: Метод вращения: метод максимального изменения нормальной дисперсии Кайзера
Описание диаграммы
Component Transformation MatrixТаблица матрицы преобразования компонентов используется для объяснения соответствия коэффициентов между основными компонентами до и после вращения.
Extraction Method: Principal Component Analysis: Метод извлечения: анализ главных компонентов
Rotation Method: Varimax with Kaiser Normalization: Метод вращения: метод максимального изменения нормальной дисперсии Кайзера
Описание диаграммы
Поворотное пространство на диаграмме компонентов (повернутая трехмерная карта главных компонентов), как видно из рисунка, наши семь переменных находятся не в одной ориентации, поэтому выделение главного компонента не может объяснить большую часть информации. Вот почему система выделяет три основных компонента.