Как найти сумму длин всех рёбер параллелепипеда
У вас возникло затруднение в решении геометрической задачи, связанной с параллелепипедом. Принципы решения таких задач, основанные на свойствах параллелепипеда, изложены в простой и доступной форме. Понять – значит решить. Подобные задачи больше не будут вызывать у вас затруднений.
Инструкция
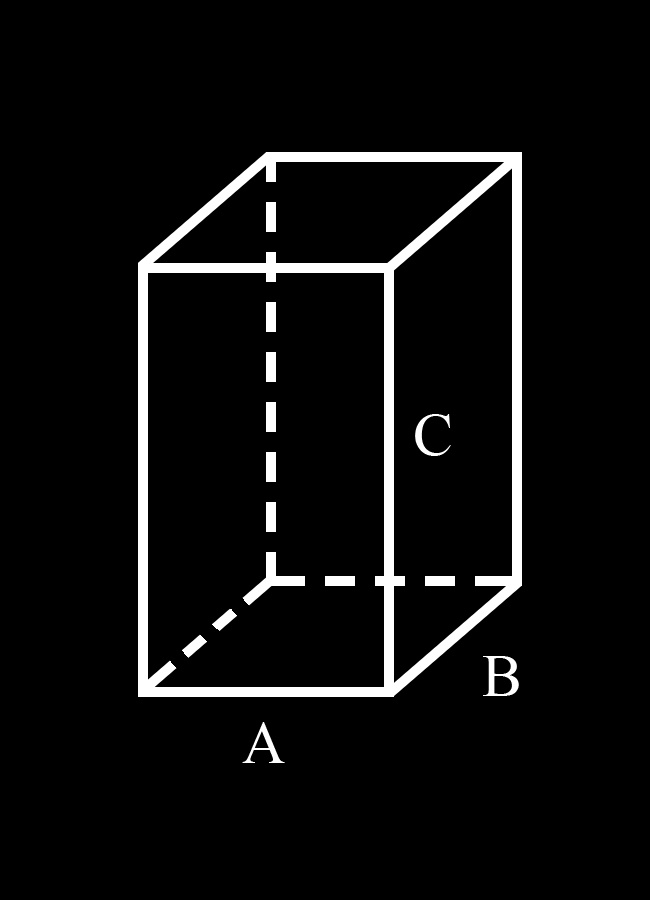
Для удобства введем обозначения:А и В стороны основания параллелепипеда; С – его боковая грань.
Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что против стороны А лежит равная ей сторона А. Поскольку противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
То же можно сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда). Ребро С одновременно является стороной двух соседних граней параллелепипеда. Поскольку противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер — 4С.
Таким образом, сумма всех ребер параллелепипеда: 4А+4В+4С или 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.
Таким образом, решение задачи относительно пространственного тела всегда можно свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Нужно просто хорошо усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.
Параллелепипед – это призма, основанием которой является параллелограмм.
Параллелепипед имеет 6 граней, и все они являются параллелограммами.
Противоположные грани равны и параллельны. Это важно.
Источники:
- сумма длин ребер прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Описание презентации по отдельным слайдам:
-
1 слайд
Прямоугольный
параллелепипед -
2 слайд
Устный счёт (повторение)
Упростите выражение2а + 7а;
8х – 7х;
5у + у
-
3 слайд
90
45
3
75
64
8
— 45
: 15
·25
— 11
:8
+ 28
36
18
: 2
90
Вычислите:
·5 -
4 слайд
Решим задачи
1.Турист прошел 15 км со скоростью 5 км/ч. Сколько времени турист был в пути?15 км за ? часов
2.Моторная лодка прошла расстояние 50 км за 2 часа. Найти скорость моторной лодки.5 км/ч
?
50 км за 2 часа -
5 слайд
Назовите формулу периметра прямоугольника?
a
b
P=4a
Назовите формулу периметра квадрата?
a
P=2(a+b) -
6 слайд
S = a · b
S = a 2
a
b
a -
-
8 слайд
16га=160000м2
160000 : 200 = 800 (м)
6а=600м2
600 : 30= 20 (м)
800 · 900 = 720000 (м2) 720000м2=72га16га
200м
?
50м
S=? (а)900м
6а
30м
?
800м
S=?(га)
50 · 30 = 1500 (м2) 1500м2=15а30м
-
-
10 слайд
Тема: Прямоугольный
параллелепипед
Цель урока:
изучить свойства прямоугольного параллелепипеда;
решение задач на нахождение площади поверхности
прямоугольного параллелепипеда. -
11 слайд
Прямоугольный параллелепипед в нашей жизни
Спичечный коробок, кирпич, шкаф, чемодан, здания, системный блок компьютера дают представление о
прямоугольном параллелепипеде. -
12 слайд
А
В
С
D
D1
С1
А1
В1
АВСDА1В1С1D1 — параллелепипед
Построение параллелепипеда
Прямоугольный параллелепипед — это тело,
все грани которого прямоугольники. -
13 слайд
Нижняя грань
верхняя грань
Поверхность прямоугольного параллелепипеда состоит из 6 граней -
14 слайд
1
2
Задняя грань
Передняя грань
Поверхность прямоугольного
параллелепипеда состоит из 6 граней -
15 слайд
Поверхность прямоугольного параллелепипеда состоит из 6 граней
боковая грань
боковая грань -
16 слайд
8
Прямоугольный параллелепипед ограничен
шестью прямоугольниками,
которые называют гранями.
Противоположные грани прямоугольного
параллелепипеда равны -
17 слайд
Стороны граней называются
ребрами параллелепипеда -
18 слайд
Равные рёбра
длина
ширина
высота
A
B
C
D
К
F
М
H -
19 слайд
Вершины граней называются
вершинами параллелепипеда -
20 слайд
длина —
ширина —
высота —Три измерения параллелепипеда
-
-
22 слайд
Какими геометрическими фигурами являются грани куба?
Куб-прямоугольный параллелепипед, у которого все измерения равны -
23 слайд
Прямоугольный параллелепипед, у которого всё ребра равны называется
К У Б
Все грани куба – равные квадраты -
24 слайд
1
2
3
Какие из фигур не могут быть развертками куба? -
25 слайд
Инструкция по изучению
суммы длин всех рёбер прямоугольного параллелепипеда
1.Покажите на модели равные рёбра.
2.По сколько равных рёбер имеет параллелепипед?
3.Как определить сумму длин всех рёбер? Сделайте вывод.
4.Вычисли длину всех рёбер по формуле
L=4а + 4в + 4с -
26 слайд
Инструкция по изучению
площади поверхности
прямоугольного параллелепипеда
1.Измерь длину, ширину и высоту модели и запиши их.
2. Вычисли площадь каждой грани (помни, что противоположные грани равны).
3.Вычисли площадь всей поверхности вашего прямоугольного параллелепипеда по формуле
Sповерхности = 2(ав +ас +вс) -
27 слайд
В ы в о д ы :
прямоугольный параллелепипед имеет:6 граней 12 рёбер 8 вершин
Грани: прямоугольники, квадраты
Sповерхности = 2(ав +ас +вс)
Сумма длин всех рёбер
L=4а + 4в + 4с -
28 слайд
L = 4α + 4b + 4c
длина всех рёбер
S = 2(αb + αc + bc)
площадь поверхности
L = 4·5 + 4·3 + 4·7 = 60 (см)
S = 2(5·3 + 5·7 + 3·7) = 2·71 = 142 (см2)
Цели и задачи урока:
- Научить учащихся отличать те из окружающих нас
тел, форма которых имеет название
“прямоугольный параллелепипед”, научить
произносить и писать этот термин и познакомить с
моделями прямоугольного параллелепипеда. - Ввести определение понятия “прямоугольный
параллелепипед”. При этом желательно избежать
заучивания формулировки определения, ученики
должны её запомнить в процессе выполнения
заданий. Одновременно они должны усвоить способ
установления принадлежности к понятию
“прямоугольный параллелепипед” с помощью
определения. - Познакомить учащихся с элементами
прямоугольного параллелепипеда: гранями,
ребрами, вершинами (запоминать определения не
требуется, достаточно, чтобы ученики умели
показывать грани, ребра и вершины различных тел,
умели рассказать своими словами, что ребра
прямоугольного параллелепипеда — это стороны
прямоугольников, вершины — концы отрезков,
являющихся ребрами). - Сформулировать понятие “смежные грани” и
“противоположные грани” (учащиеся должны уметь
указать на наличие общего ребра при обосновании
того, что грани смежные, и на отсутствие общих
ребер при доказательстве того, что грани
противоположные, заучивать формулировки не
надо). - Познакомить учащихся с понятиями “измерения
прямоугольного параллелепипеда”, “высота
прямоугольного параллелепипеда” (каждый ученик
должен уметь показать измерения
параллелепипеда, понимать, что высотой может
служить любое измерение). - Научить достраивать изображения
прямоугольного параллелепипеда и строить
изображение самостоятельно. - Дать представление о развертке прямоугольного
параллелепипеда.
План урока
- Организационный момент.
- Постановка целей и задач урока.
- Актуализация опорных знаний и умений учащихся.
a. Устный счет — математическое лото.
b. Логическое упражнение.
c. Блиц-опрос. - Изучение нового материала.
- Практическая работа.
- Самостоятельная работа.
- Итог урока.
ХОД УРОКА
I. Организационный момент
Добрый день, дорогие путешественники в страну
знаний!
Чтобы начать сегодняшний урок, мне хотелось бы
узнать, готовы ли вы к уроку, какое у вас
настроение, есть ли у вас желание узнать что-то
новое на сегодняшнем уроке?
Как сказал древнегреческий философ Саади:
“Ученик, который учится без желания — это птица
без крыльев”.
И мне бы хотелось, чтобы было у вас желание
учиться, узнавать что-то новое, неопознанное не
только на сегодняшнем уроке, а всегда и только в
этом случае своими “крыльями” будете
“взлетать” все выше и выше.
А также мне очень хочется обратиться к словам
известного российского математика А.И.
Мордковича: “Кто с детских лет занимается
математикой, этот развивает внимание, тренирует
свой мозг, свою волю, воспитывает в себе
настойчивость и упорство в достижении цели”.
Именно это нам потребуется на сегодняшнем
уроке: внимание, настойчивость и упорство, чтобы
достичь поставленных целей.
II. Постановка целей и задач урока
III. Актуализация опорных знаний и умений
учащихся
a. Устный счет — математическое лото
Ребята, для того, чтобы приступить к
рассмотрению нашего вопроса мы должны вспомнить
материал, который нам поможет в процессе
изучения новой темы. Для этого давайте решим
примеры цепочкой.
(На доске вывешивается таблица с примерами для
устного счета, у учащихся карточки с
соответствующими ответами. В процессе
правильного решения примеров на таблице
формируется рисунок, — теневой фон
Ново-Иерусалимского монастыря, — состящий из
геометрических фигур.)
|
52 : 2 |
+ 24 |
: 25 |
|
х 36 |
: 18 |
х12 |
|
+34 |
: 12 |
+ 56 |
| -38 |
: 2 |
х100 |
Ребята, внимательно посмотрите на полученный
рисунок.
Что он вам напоминает?
Ново-Иерусалимский монастырь, который основан
Патриархом Никоном в 1653 году при царе Алексее
Михайловиче Романове. Монастырь строился 8 лет по
макету, привезенному из города Иерусалима
Израиля.
Правильно, а посмотрите внимательно, само
здание церкви на рисунке из чего складывалось у
нас?
Назовите именно из каких геометрических фигур?
Многие здания на рисунках напоминают нам
какие-то геометрические фигуры.
А что же представляют они собой в
действительности?
(Двум ученикам предлагается собрать модель
монастыря из предложенных геометрических тел, в
это же время с остальными учащимися продолжается
работа).
b. Логическое упражнение
Назовите лишнее слово: треугольник, квадрат,
площадь, круг, прямоугольник.
c. Блиц-опрос
- Прямоугольник — это …
- а и в — …
- а — это …
- в — это …
- Площадь прямоугольника равна …
- Выражение Р = 2х(а+в) называется …
- Прямоугольник, у которого длина и ширина равны,
называется … - У равных фигур площади и периметры …
- Если фигура разбита на части, то площадь фигуры
равна …
Обратите внимание на модель монастыря.
В основном отдельные части здания монастыря
напоминают нам коробку. (Продемонстрировать).
IY. Изучение нового материала
В действительности мы часто встречаем
предметы, имеющие похожую форму. Они могут быть
сделаны из разного материала и окрашены в разные
цвета, но по форме они напоминают друг друга.
Например: чемодан, шкаф, телевизор и т.д.
Эти предметы имеют похожую форму. Правда они
отличаются мелкими деталями: у чемодана есть
ручка, у шкафа — двери, но если не обращать
внимание на эти мелкие детали, то можно сказать,
что все эти предметы имеют примерно одинаковую
форму. Все они напоминают по форме изображенный
на рисунке предмет, не имеющий никаких
второстепенных деталей. Изображенное тело
называется прямоугольный параллелепипед. (Данное
словосочетание — “прямоугольный
параллелепипед” — написано на доске и его дети
читают хором).
Приведите примеры предметов, которые имеют
форму прямоугольного параллелепипеда.
А сейчас давайте познакомимся с его элементами.
Обращенная к нам сторона этого тела имеет форму
прямоугольника.
Если внимательно посмотреть на это тело, то мы
заметим, что вся поверхность прямоугольного
параллелепипеда состоит из прямоугольников,
которые называются его гранями.
Ответьте, сколько граней имеет прямоугольный
параллелепипед?
Стоит запомнить какая грань как называется: та
грань, которая обращена к нам называется
передней, точно такая же грань имеется сзади — это
задняя грань, боковые грани — левая и правая. Та
грань, которая сверху, называется верхняя, а
грань, на которой фигура стоит, называется нижней
или основанием.
Стороны прямоугольников, которые являются
гранями прямоугольного параллелепипеда,
называются ребрами этого прямоугольного
параллелепипеда.
Выясните самостоятельно, сколько ребер имеет
прямоугольный параллелепипед.
Вершины граней являются вершинами
параллелепипеда.
Самостоятельно посчитайте, сколько имеет
вершин прямоугольный параллелепипед.
Две грани прямоугольного параллелепипеда, не
имеющие общих ребер, называются
противоположными. Противоположные грани всегда
равны.
Две грани прямоугольного параллелепипеда,
имеющие общее ребро, называются смежными
гранями.
Из каждой вершины прямоугольного
параллелепипеда выходят три ребра. Длины этих
ребер — длина, ширина и высота прямоугольного
параллелепипеда, или его измерения.
Прямоугольный параллелепипед, все ребра
которого равны, называется кубом. Все грани куба —
равные квадраты.
Мы с вами, таким образом, познакомились с
прямоугольным параллелепипедом и его
элементами.
Осталось нам научиться строить модель
прямоугольного параллелепипеда, а поможет нам в
этом алгоритм построения параллелепипеда.
Алгоритм построения прямоугольного
параллелепипеда
1. Построить прямоугольник заданной длины (а) и
высоты (h).
2. Из каждой вершины отложить отрезок, равный
половине ширины (в) под углом 45 градусов.
3. Соединить концы отрезков, причем невидимые
грани — пунктирной линией.
Развертка прямоугольного
параллелепипеда.
Нетрудно из 6 бумажных прямоугольников склеить
закрытую коробочку, представляющую собой
поверхность прямоугольного параллелепипеда. А
что же получится, если наоборот разрезать
поверхность вдоль всех ребер? Она снова
распадется на 6 прямоугольников. Но мы произведем
разрез осторожнее, не по всем ребрам. Сначала мы
разрежем поверхность прямоугольного
параллелепипеда по трем ребрам, принадлежащим
верхнему основанию. Тогда верхнее основание
можно будет приоткрыть, как крышку. После этого
мы разрежем поверхность по четырем параллельным
ребрам, которые являются высотами. Теперь
оставшуюся поверхность легко раскрыть и затем
превратить в плоский кусок бумаги. Мы как бы
развернули поверхность прямоугольного
параллелепипеда. Если теперь обратно произвести
все сгибы, а затем проклеить ребра, по которым
производились разрезы, то из фигуры мы снова
получим поверхность прямоугольного
параллелепипеда. Фигура, изображенная на
рисунке, называется разверткой прямоугольного
параллелепипеда.
Y. Практическая работа
- Используя алгоритм построения прямоугольного
параллелепипеда, построить прямоугольный
параллелепипед заданных измерений. Длина — 4 см,
высота — 5 см, ширина — 3 см. Обозначьте красным
карандашом вершины прямоугольного
параллелепипеда. Выпишите переднюю грань. - На каждой парте модель прямоугольного
параллелепипеда и инструкция по изучению
площади поверхности прямоугольного
параллелепипеда.
- В практике очень важно знать общую длину всех
ребер прямоугольного параллелепипеда.
ИНСТРУКЦИЯ ПО ИЗУЧЕНИЮ ПЛОЩАДИ
ПОВЕРХНОСТИ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
1. Измерь длину, ширину, высоту модели и запиши
их.
2. Вычисли площадь каждой грани модели.
3. Сделайте вывод о площадях противоположных
граней и запишите его.
4. Вычислите площадь всей поверхности вашего
прямоугольного параллелепипеда.
Сделайте вывод.
ИНСТРУКЦИЯ ПО ИЗУЧЕНИЮ СУММЫ ДЛИН
ВСЕХ РЕБЕР ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
1. Покажите на модели равные ребра.
2. Сколько всего пар равных ребер?
3. Как определить сумму длин всех ребер?
Сделайте вывод. Запишите формулу.
YI. Самостоятельная работа
Результаты самостоятельной работы проверяются
на уроке.
Вычислите общую длину всех ребер
прямоугольного параллелепипеда, если его
измерения равны: а — 135, 25 см., в — 93,5 см., с — 178 см.
YII. Итог урока
Итог урока проводится по опорному конспекту,
который демонстрируется на протяжении всего
урока по этапам ознакомления с изучаемым
материалом.
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД ИМЕЕТ:
12 ребер
8 вершин
Грани: прямоугольники; квадраты.
S поверхности: 2(ав + ас + вс); 6аа
Сумма длин всех ребер: 4(а + в + с); 12а
Разделы презентаций
- Разное
- Бизнес и предпринимательство
- Образование
- Финансы
- Государство
- Спорт
- Армия
- Культурология
- Еда и кулинария
- Лингвистика
- Черчение
- Психология
- Социология
- Английский язык
- Астрономия
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Экология
- Экономика
- Юриспруденция
Презентация на тему Прямоугольный параллелепипед
Содержание
-
1.
Прямоугольный параллелепипед -
2.
Цель урока: Научиться определять вершины, ребра, грани -
3.
Прямоугольный параллелепипед Это параллелепипед, у которого все грани прямоугольники -
5.
А В С D1 -
6.
Свойства прямоугольного параллелепипеда: АВСDА1В1С1D1 — параллелепипед А -
7.
Запишите все грани прямоугольного параллелепипеда -
8.
a – длина b – ширина c — высота -
9.
c -
10.
Развертка прямоугольного параллелепипеда -
11.
Какие из фигур
могут быть развёртками
прямоугольного параллелепипеда? 1 2 3 4 -
13.
Вершин — 8 Ребер — 12 Граней — 6 Куб -
14.
a -
15.
2 3 Какие из фигур не могут быть развертками куба? -
16.
Инструкция по изучению
суммы длин всех -
17.
Инструкция по изучению площади поверхности прямоугольного параллелепипеда -
18.
6 граней 12 рёбер -
19.
L = 4α + 4b -
20.
Задача 1 На рисунке изображен прямоугольный параллелепипед -
21.
Задача 2 Измерения прямоугольного параллелепипеда MNKPEFST равны -
22.
Задача 3 Вычислите площадь поверхности и сумму -
23.
Спасибо за урок ! -
24.
Скачать презентацию -
25.
Похожие презентации
Цель урока: Научиться определять вершины, ребра, грани прямоугольного параллелепипеда и куба; Находить длину ребер и площадь S поверхности прямоугольного параллелепипеда
Слайды и текст этой презентации
Слайд 1
Сегодня на уроке вы узнаете:
Что такое прямоугольный параллелепипед;
Сколько

ребер, вершин, граней у параллелепипеда. Их свойства;
Что такое куб.
Формулу
площади S поверхности прямоугольного параллелепипеда.
Слайд 2
Цель урока:
Научиться определять вершины, ребра, грани прямоугольного параллелепипеда

и куба;
Находить длину ребер и площадь S поверхности прямоугольного
параллелепипеда
Слайд 3
Прямоугольный параллелепипед
Это параллелепипед, у которого все грани

прямоугольники
Слайд 5
А
В
С
D1
С1
Вершины – точки. Вершин 8.

Грани – прямоугольники. Поверхность прямоугольника состоит из 6 граней.
Ребра
– отрезки, стороны граней. Рёбер у прямоугольного параллелепипеда 12.
А1
D
В1
Слайд 6
Свойства прямоугольного параллелепипеда:
АВСDА1В1С1D1 — параллелепипед
А
В
С
D
D1
С1
А1
В1
Грани АА1В1В и DD1С1С

не имеют общих вершин. Такие грани называют противолежащие.
Грани ABCD
и A1B1C1D1 , а также грани AA1 D1D и BB1C1C
– противолежащие грани.
Противолежащие грани прямоугольного параллелепипеда равны.
Слайд 7
Запишите все грани прямоугольного параллелепипеда

Слайд 8
a – длина
b – ширина
c — высота

Слайд 9
c
S=2ab
S=2(ab + ac+ bc)
L=4(a + b +

c)
L=4a
b
Площадь поверхности:
Длина ребер:
+2bc
+2ac
+4b
+4c
Площадью поверхности параллелепипеда называют сумму площадей
всех его граней.
a
Слайд 10
Развертка прямоугольного параллелепипеда

Слайд 11
Какие из фигур
могут быть развёртками
прямоугольного параллелепипеда?
1
2
3
4

Слайд 13
Вершин — 8
Ребер — 12
Граней — 6
Куб

Слайд 14
a
S=6a2
L=12a
Площадь поверхности куба:
Длина ребер куба:
a
a

Слайд 15
2
3
Какие из фигур не могут быть развертками куба?

Слайд 16
Инструкция по изучению
суммы длин всех рёбер прямоугольного

параллелепипеда
1.Покажите на модели равные рёбра.
2.По сколько равных рёбер имеет
параллелепипед?
3.Как определить сумму длин всех рёбер? Сделайте вывод.
4.Вычисли длину всех
рёбер по формуле
L=4а + 4b + 4с
Слайд 17
Инструкция по изучению площади поверхности прямоугольного параллелепипеда
1.Измерь длину,

ширину и высоту модели и запиши их.
2. Вычисли площадь
каждой грани (помни, что противоположные грани равны).
3.Вычисли площадь всей поверхности
вашего прямоугольного параллелепипеда по формуле
Sповерхности = 2(аb +ас +bc)
Слайд 18
6 граней 12 рёбер 8

вершин
Грани: прямоугольники, квадраты
Sповерхности = 2(аb +ас +bc)
Сумма длин всех
рёбер
L=4а + 4b + 4с
Выводы:
прямоугольный параллелепипед
имеет:
Слайд 19
L = 4α + 4b + 4c
длина всех

рёбер
S = 2(αb + αc + bc)
площадь поверхности
L =
4·5 + 4·3 + 4·7 = 60 (см)
S = 2(5·3
+ 5·7 + 3·7) = 2·71 = 142 (см2)
Слайд 20
Задача 1
На рисунке изображен прямоугольный параллелепипед ABCDMNKP. Запишите:
Грани,

которым принадлежит вершина С;
Рёбра, равные ребру BC;
Верхнюю грань;
Вершины, принадлежащие
нижней грани;
Грани, имеющие общее ребро AM;
Грань, равную грани DPKC
Слайд 21
Задача 2
Измерения прямоугольного параллелепипеда MNKPEFST равны 9 см,

5 см и 6 см. Вычислите сумму всех его
ребер и площади его поверхности.
6 см
9 см
5 см
Слайд 22
Задача 3
Вычислите площадь поверхности и сумму длин всех

рёбер куба, ребро которого равно 7 см.
Как обнаружить сумму длин всех рёбер параллелепипеда
У вас появилось затруднение в решении геометрической задачи, связанной с параллелепипедом. Тезисы решения таких задач, основанные на свойствах параллелепипеда , высказаны в примитивный и доступной форме. Осознать – значит решить. Сходственные задачи огромнее не будут вызывать у вас сложностей.
Инструкция
1. Для комфорта введем обозначения:А и В стороны основания параллелепипеда ; С – его боковая грань.
2. Таким образом, в основании параллелепипеда лежит параллелограмм со сторонами А и В. Параллелограмм – это четырехугольник, противоположные стороны которого равны и параллельны. Из этого определения следует, что супротив стороны А лежит равная ей сторона А. От того что противолежащие грани параллелепипеда равны (вытекает из определения), то верхняя его грань тоже имеет 2 стороны равные А. Таким образом, сумма всех четырех этих сторон равна 4А.
3. То же дозволено сказать и о стороне В. Противоположная ей сторона в основании параллелепипеда равна В. Верхняя (противолежащая) грань параллелепипеда тоже имеет 2 стороны, равные В. Сумма всех четырех этих сторон равна 4В.
4. Боковые грани параллелепипеда тоже являются параллелограммами (вытекает из свойств параллелепипеда ). Ребро С единовременно является стороной 2-х соседних граней параллелепипеда . От того что противоположные грани параллелепипеда попарно равны, то все его боковые ребра равны между собой и равны С. Сумма боковых ребер – 4С.
5. Таким образом, сумма всех ребер параллелепипеда : 4А+4В+4С либо 4(А+В+С)Частный случай прямого параллелепипеда – куб. Сумма всех его ребер равна 12А.Таким образом, решение задачи касательно пространственного тела неизменно дозволено свести к решению задач с плоскими фигурами, на которое это тело разбивается.
Полезный совет
Вычислить сумму всех ребер параллелепипеда – задача несложная. Надобно примитивно отменно усвоить, что представляет собой данное геометрическое тело, и знать его свойства. Решение задачи вытекает из самого определения параллелепипеда.Параллелепипед – это призма, основанием которой является параллелограмм. Параллелепипед имеет 6 граней, и все они являются параллелограммами. Противоположные грани равны и параллельны. Это главно.




























