Вопросы
для подготовки к экзамену по дисциплине
«Информатика»
Наша учеба, работа, личные дела — это
каждодневное, ежечасное решение различных
задач. Каждая задача требует для своего
решения выполнения определенных
действий. Многократно решая задачи,
можно заметьть, что необходимые действия
должны выполняться в строго определенном
порядке. В таких случаях принято говорить
об алгоритме решения задач. Понятие
алгоритма считается одним из древнейших.
Оно возникло задолго до появления ЭВМ,
но с развитием вычислительной техники
его роль значительно возросла.
Происхождение понятия алгоритма связано
с именем великого среднеазиатского
ученого Аль Хорезми, жившего в 9 веке
н.э. Им были сформулированы впервые
правила выполнения четырех арифметических
действий.
Алгоритм — это точная инструкция, а
инструкции встречаются во всех областях
человеческой деятельности. Однако не
всякую инструкцию можно назвать
алгоритмом. Решая задачу, человек часто
не задумывается над тем, как он это
делает, и порой, затрудняется записать
последовательность выполняемых действий.
Но для того, чтобы поручить решение
задачи автоматическому устройству
необходимо составить алгоритм с четким
указанием последовательности действий.
Чтобы автоматическое устройство могло
решить задачу в соответствии с алгоритмом,
оно должно понимать каждое указание
алгоритма. Алгоритм применяется к
искомому набору исходных величин,
называемых аргументами. Цель исполнения
алгоритма получение определенного
результата, если в результате исполнения
алгоритма не достигнута определенная
цель, значит алгоритм либо неверен, либо
не завершен.
Алгоритмом называется точная инструкция
исполнителю в понятной для него форме,
определяющая процесс достижения
поставленной цели на основе имеющихся
исходных данных за конечное число шагов.
Основными свойствами алгоритмов
являются:
1. Универсальность (массовость)
— применимость алгоритма к различным
наборам исходных данных.
2. Дискретность — процесс решения
задачи по алгоритму разбит на отдельные
действия.
3. Однозначность — правила и порядок
выполнения действий алгоритма имеют
единственное толкование.
4. Конечность — каждое из действий и
весь алгоритм в целом обязательно
завершаются.
5. Результативность — по завершении
выполнения алгоритма обязательно
получается конечный результат.
6. Выполнимость — результата алгоритма
достигается за конечное число шагов.
Алгоритм считается правильным, если
его выполнение дает правильный результат.
Соответственно алгоритм содержит
ошибки, если можно указать такие
допустимые исходные данные или условия,
при которых выполнение алгоритма либо
не завершится вообще, либо не будет
получено никаких результатов, либо
полученные результаты окажутся
неправильными.
Выделяют три крупных класса алгоритмов:
— вычислительные алгоритмы, работающие
со сравнительно простыми видами данных,
такими как числа и матрицы, хотя сам
процесс вычисления может быть долгим
и сложным;
— информационные алгоритмы,
представляющие собой набор сравнительно
простых процедур, работающих с большими
объемами информации (алгоритмы баз
данных);
— управляющие алгоритмы, генерирующие
различные управляющие воздействия на
основе данных, полученных от внешних
процессов, которыми алгоритмы управляют.
Для записи алгоритмов используют самые
разнообразные средства. Выбор средства
определяется типом исполняемого
алгоритма. Выделяют следующие основные
способы записи алгоритмов:
— вербальный, когда алгоритм описывается
на человеческом языке;
— символьный, когда алгоритм описывается
с помощью набора символов;
— графический, когда алгоритм
описывается с помощью набора графических
изображений.
Общепринятыми способами записи являются
графическая запись с помощью блок-схем
и символьная запись с помощью какого-либо
алгоритмического языка.
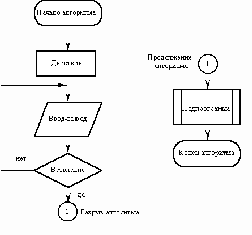
Описание алгоритма с помощью блок схем
осуществляется рисованием последовательности
геометрических фигур, каждая из которых
подразумевает выполнение определенного
действия алгоритма. Порядок выполнения
действий указывается стрелками. Написание
алгоритмов с помощью блок-схем
регламентируется ГОСТом. Внешний вид
основных блоков, применяемых при
написании блок схем, приведен на рисунке:
В зависимости от последовательности
выполнения действий в алгоритме выделяют
алгоритмы линейной, разветвленной и
циклической структуры.
В алгоритмах линейной структуры действия
выполняются последовательно одно за
другим:
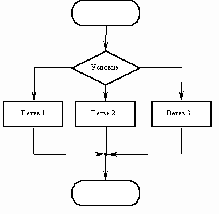
В алгоритмах разветвленной структуры в
зависимости от выполнения или невыполнения
какого-либо условия производятся
различные последовательности действий.
Каждая такая последовательность действий
называется ветвью алгоритма.
В алгоритмах циклической структуры в
зависимости от выполнения или невыполнения
какого-либо условия выполняется
повторяющаяся последовательность
действий, называющаяся телом
цикла. Вложенным называется цикл,
находящийся внутри тела другого цикла.
Различают циклы с предусловием и послеусловием:
Итерационным называется цикл, число
повторений которого не задается, а
определяется в ходе выполнения цикла.
В этом случае одно повторение цикла
называется итерацией.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цели урока:
- познакомить с понятием алгоритма, исполнителем
алгоритма, видами исполнителя, средой, СКИ и
системой отказов исполнителя, свойствами
алгоритма, показать среду, СКИ и систему отказов
для конкретного исполнителя, - развивать умение работать самостоятельно,
творчески. - воспитывать нравственное отношение к труду.
ХОД УРОКА
Презентация 1
В течение всей жизни каждый человек постоянно
пользуется набором всевозможных алгоритмов —
правил, которые заложены природой, даны
воспитанием, обучением, тренировкой, выработаны
на основе собственного опыта. Инструкции, в
которых указано, как пользоваться лифтом,
телефоном, различными автоматами и бытовыми
приборами, правила перехода улицы, оказания
первой медицинской помощи, распорядок дня,
кулинарные рецепты, порядок проведения
химического опыта, правила вычислений, методы
решения алгебраических и геометрических задач —
все это можно считать алгоритмами. Таким образом,
все мы живем в мире алгоритмов. Алгоритмы
экономят силы и время человека, так как однажды
усвоенным правилом (алгоритмом) он может
пользоваться всю жизнь.
Приведите пример алгоритма перехода дороги с
светофором, и без светофора.
Ваш мозг постоянно занят работой, поиском
решений. Говорят, что человек составляет
алгоритм.
Тема нашего сегодняшнего урока. Алгоритм.
Свойства алгоритма.
Учащиеся записывают тему урока (с
презентации).
На экране вы видите команды, необходимо
составить алгоритм заваривания чая.
Работа идет со всем классом, учащиеся
обсуждают о выборе последовательности команд,
учитель на доске регистрирует их ответ.
- размешать сахар ложечкой;
- добавить кипятку;
- налить в чашку заварку;
- вскипятить воду;
- положить сахар.
У вас должен был получиться такой алгоритм:
- вскипятить воду;
- налить в чашку заварку;
- добавить кипятку;
- положить сахар;
- размешать сахар ложечкой;
В природе все взаимосвязано, все на все влияет и
все зависит друг от друга. Складываются сложные
цепочки событий. Если вынуть хоть одно звено, вся
цепочка разорвется.
Как вы думаете, что будет если убрать из рецепта
вторую команду? А четвертую?
Надо научится выстраивать в нужном порядке все
звенья какой-нибудь жизненной или
математической задачи. Эти умения нужны и при
обработке информации. Информацию следует
обрабатывать по определенным правилам, которые
выполняются в определенном порядке.
Итак, давайте с вами, попробуем дать
определения понятию алгоритм.
Учащиеся формулируют и записывают с доски.
Алгоритм – понятное и точное
предписание исполнителю совершить
последовательность действий, направленных на
достижение указанной цели или на решение
поставленной задачи.
Учащиеся записывают в тетрадь определение.
Синонимы слова «алгоритм»:
- план;
- инструкция;
- рецепт;
- предписание.
Происхождение термина «алгоритм» связывают с
именем великого узбекского математика и
астронома аль-Хорезми (жившего в IX в.). Абу
Абдуллах Мухаммад ибн Муса аль-Хорезми (ок. 783,
Хива , Хорезм — ок. 850, Багдад) — один из
крупнейших средневековых ученых (математик,
астроном, географ и историк) IX века, основатель
классической алгебры.
Ал-Хорезми известен прежде всего своей «Книгой о
восполнении и противопоставлении» («Аль-китаб
аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»),
которая сыграла важнейшую роль в истории
математики. От названия этой книги произошло
слово «алгебра».
В своих трудах по арифметике и алгебре он
разработал, в частности, правила выполнения
четырех арифметических операций над
многозначными десятичными числами. Эти правила
определяют последовательность действий, которые
необходимо выполнить, чтобы получить сумму
чисел, произведение и т. д. Почти в таком же виде
эти правила изучаются всеми школьниками в
начальных классах.
Латинский перевод книги начинается словами
«Dixit Algorizmi» (сказал Алгоризми). Так как сочинение
об арифметике было очень популярно в Европе, имя
автора (Algorizmi или Algorizmus) стало нарицательным и
средневековые математики так называли
арифметику, основанную на десятичной
позиционной системе счисления. Позднее
европейские математики стали называть так
всякую систему вычислений по определенному
правилу. В настоящее время термин «алгоритм»
означает набор инструкций, описывающих порядок
действий исполнителя для достижения результата
решения задачи за конечное число действий.
Затем понятие алгоритма переместилось в
область логики, где появилась теория алгоритмов,
изучавшая процесс доказательств или
разрешимость и неразрешимость математических
задач. В 1937 году, когда английский
математик Алан Тьюринг доказал
теоретически возможность построения устройства,
осуществляющего алгоритм. Такое абстрактное
устройство получило название МАШИНА ТЬЮРИНГА.
Аналогичный, но более простой исполнитель
алгоритма – МАШИНА ПОСТА. Когда же были
созданы первые ЭВМ, понятие алгоритма и теория
алгоритмов переместились в новую науку,
связанную с этими вычислительными устройствами
– информатику.
Приведите примеры алгоритмов.
А теперь скажите кто может выполнить данный
алгоритм?
Приведите пример алгоритмов с разными
исполнителями.
Получается, всякий алгоритм составляется в
расчете на определенного исполнителя. Им может
быть человек, робот, компьютер и др. Чтобы
составить алгоритм для исполнителя, нужно знать,
какие команды исполнитель может понять и
исполнить, а какие нет.
Исполнитель – объект, который будет выполнять
алгоритм.
Приведите примеры исполнителей и что они
могут делать.
В классе исполнителей выделяют два типа:
формальные, неформальные. Формальный
исполнитель одну и ту же команду всегда выполнит
одинаково, неформальный может выполнять команду
по-разному. Неформальный исполнитель – человек,
формальный – технические устройства.
У каждого исполнителя можно выделить: среду
исполнителя, систему команд исполнителя, систему
отказов.
Среда – обстановка, в которой
работает исполнитель.
Система команд исполнителя (СКИ) –
совокупность команд, которую исполнитель умеет
выполнять.
Система отказов – ситуации сбоя
работы исполнителя, которые возникают, если
команда вызывается пpи недопустимом для нее
состоянии сpеды («не понимаю», «не могу»).
«Не понимаю» – возникает тогда, когда
исполнителю дается команда не входящая в его СКИ,
«не могу» – когда команда из СКИ не может быть
выполнена в конкретных условиях среды.
Укажите для данных примеров среду, ски,
систему отказов.
Свойства алгоритмов
1. Как мы уже знаем, алгоритм задает полную
последовательность действий, которые необходимо
выполнять для решения задачи. При этом, как
правило, для выполнения этих действий их
расчленяют (разбивают) в определенной
последовательности на простые шаги. Возникает
упорядоченная запись совокупности четко
разделенных предписаний (директив, команд),
образующих прерывную (или, как говорят,
дискретную) структуру алгоритма. Выполнить
действия следующего предписания можно лишь
выполнив действия предыдущего.
Под ДИСКРЕТНОСТЬЮ понимают возможность
разбиения алгоритма на отдельные элементарные
действия, выполнение которых человеком или
машиной не вызывает сомнения.
Пример по алгоритму заваривая чая
2. Чтобы исполнитель сумел решить поставленную
перед ним задачу, используя алгоритм, он должен
уметь выполнить каждое его указание. Иными
словами, он должен понимать суть управления. То
есть при составлении алгоритма нужно
обязательно учитывать «правила игры», т.е.
систему предписаний (или систему команд), которые
понимает ЭВМ. Мы будем говорить в данном случае о
«понятности» алгоритма.
Под «ПОНЯТНОСТЬЮ» алгоритмов понимают
указания, которые понятны исполнителю.
Пример по пришиванию пуговицы.
3. Будучи понятным, алгоритм не должен все же
содержать предписаний, смысл которых может
восприниматься неоднозначно. Этими свойствами
часто не обладают предписания и инструкции,
которые составляются для людей.
Например, вспомним известную всем притчу о
царской воле. Царь приказал подчиненным
выполнить такой указ: «Казнить нельзя
помиловать». Он забыл в указе поставить
запятую, а подчиненные не знали, что им делать.
Указание «казнить нельзя, помиловать» и
«казнить, нельзя помиловать» задают совсем
разные действия, от которых зависит жизнь
человека.
Кроме того, в алгоритмах недопустимы такие
ситуации, когда после выполнения очередного
предписания алгоритма исполнителю неясно, какое
из них должно выполняться на следующем шаге.
Под ОДНОЗНАЧНОСТЬЮ алгоритмов понимается
единственность толкования правил выполнения
действий и порядка их выполнения.
Пример, фрагмент мультфильма «Стран
невыученных уроков».
4. Очень важно, чтобы составленный алгоритм
обеспечивал решение не одной частной задачи, а
мог выполнять решение широкого класса задач
данного типа.
Алгоритм можно использовать для любого
квадратного у равнения. Такой алгоритм будет
МАССОВЫЙ.
Пример с чайниками, обогревателями.
5. Под КОНЕЧНОСТЬЮ алгоритмов понимают
завершение работы алгоритма в целом за конечное
число шагов.
Пример с ловлей рыбы.
6. Еще к желательным свойствам алгоритмов нужно
отнести РЕЗУЛЬТАТИВНОСТЬ, она предполагает, что
выполнение алгоритмов должно завершаться
получением определенных результатов.
Подобные ситуации в информатике возникают, когда
какие-либо действия невозможно выполнить. В
математике такие ситуации называют
неопределенностью. Например, деление числа на
ноль, извлечение квадратного корня из
отрицательного числа, да и само понятие
бесконечности неопределенно. Поэтому, если
алгоритм задает бесконечную последовательность
действий, то в этом случае он также считается
результатом неопределенным.
Но можно действовать по-другому. А именно:
указать причину неопределенного результата. В
таком случае, пояснения типа «на ноль делить
нельзя», «компьютер выполнить такое не в
состоянии» и т.п. можно считать результатом
выполнение алгоритма.
Таким образом, свойство результативности
состоит в том, что во всех» случаях можно
указать, что мы понимаем под результатом
выполнения алгоритма.
Пример с нахождением стрелы Ивана Царевича у
лягушки.
7. И последнее общее свойство алгоритмов – их
правильность.
Мы говорим, что алгоритм ПРАВИЛЬНЫЙ, если его
выполнение дает правильные результаты решения
поставленных задач.
Соответственно мы говорим, что алгоритм СОДЕРЖИТ
ОШИБКИ, если можно указать такие допустимые
исходные данные или условия, при которых
выполнение алгоритма либо не завершится вообще,
либо не будет получено никаких результатов, либо
полученные результаты окажутся неправильными.
Пример с арифметическим выражением.
Вывод:
Основные свойства алгоритмов:
- дискретность;
- понятность;
- однозначность;
- массовость;
- результативность;
- конечность;
- правильность.
Учащиеся записывают в тетрадь свойства.
Решение задач на определение свойств.
Обсуждение свойств с классом.
Задание 1.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция по варке манной каши
Молоко вскипятить добавить соль, сахар, засыпать
тонкой струйкой, непрерывно помешивая манную
крупу, довести до кипения, прокипятить минут 5-7,
добавить масло и дать остыть.
Нет понятности: какое количество (в граммах)
брать продуктов.
Возможный исправленный вариант
- Включить плиту
- Влить в кастрюлю 1,5 литра молока
- Добавить 5 грамм соли, 15 грамм сахара
- Довести молоко до кипения
- 8 столовых ложек манной крупы засыпать тонкой
струйкой, непрерывно помешивая молоко - Довести до кипения
- Кипятить 5 минут
- Добавить 20 грамм сливочного масла
- Выключить плиту, снять с плиты кастрюлю.
Задание 2.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция нахождения большего из двух данных
чисел.
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше
Нет результативности. Что делать в том случае,
если А=В?
Возможный исправленный вариант
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше - Если получился ноль, сообщить, что числа равны
Задание 3.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция покраски забора
- Покрасить первую доску.
- Переместиться к следующей доске.
- Перейти к действию 1.
Нет конечности. Что делать в том случае, когда
доски закончились?
Возможный исправленный вариант
- Покрасить первую доску.
- Если есть еще доска, переместиться к следующей
доске. - Перейти к действию 1.
- Если доски закончились, завершить работу.
Практическая работа в парах (5 мин.)
Приложение 1
Задание 1. Исправьте алгоритм
«Получения кипятка», чтобы предотвратить
несчастный случай.
Задание 2. Используя представленные
команды, составить алгоритм покраски мяча
Задание 3. Составить инструкцию, в
которой не выполняется хотя бы одно свойство
алгоритма. Записать какие изменения нужно в нее
внести, чтобы получить алгоритм.
Тест самопроверкой (5 мин.)
1. Алгоритм – это:
А) Указание на выполнение действий,
Б) Система правил, описывающая
последовательность действий, которые необходимо
выполнить для решения задачи,
В) Процесс выполнения вычислений, приводящих к
решению задачи
2. Свойство алгоритма – дискретность, выражает,
что:
А) Команды должны следовать последовательно
друг за другом,
Б) Каждая команда должна быть описана в расчете
на конкретного исполнителя,
В) Разбиение алгоритма на конечное число команд
3. Среда исполнителя – это:
А) Обстановка, в которой работает исполнитель.
Б) Объект, который будет выполнять алгоритм
В) Совокупность команд, которую исполнитель
умеет выполнять.
4. В расчете на кого должен строиться алгоритм:
А) В расчете на ЭВМ,
Б) В расчете на умственные способности товарища,
В) В расчете на конкретного исполнителя
5. Какое из перечисленных свойств относится к
свойствам алгоритма:
А) Визуальность,
Б) Совокупность,
В) Понятность
6. Исполнитель «человек» – это
А) Формальный исполнитель
Б) Неформальный исполнитель
В) Нормальный исполнитель
Проверка теста.
Подведение итогов (5 мин.)
Домашнее задание:
1. Выучить теоретический материал
2. Привести 3 примера алгоритмов для различных
исполнителей.
3. Составить 2 инструкции, в которых не
выполняется хотя бы одно свойство алгоритма.
Записать какие изменения нужно в них внести,
чтобы получить алгоритм.
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
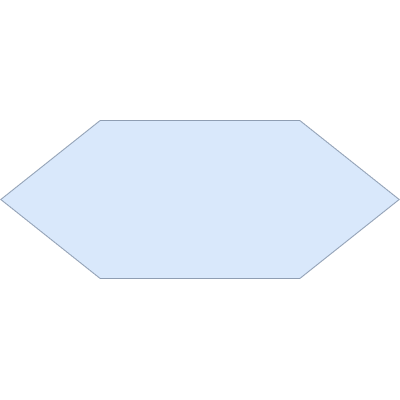
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
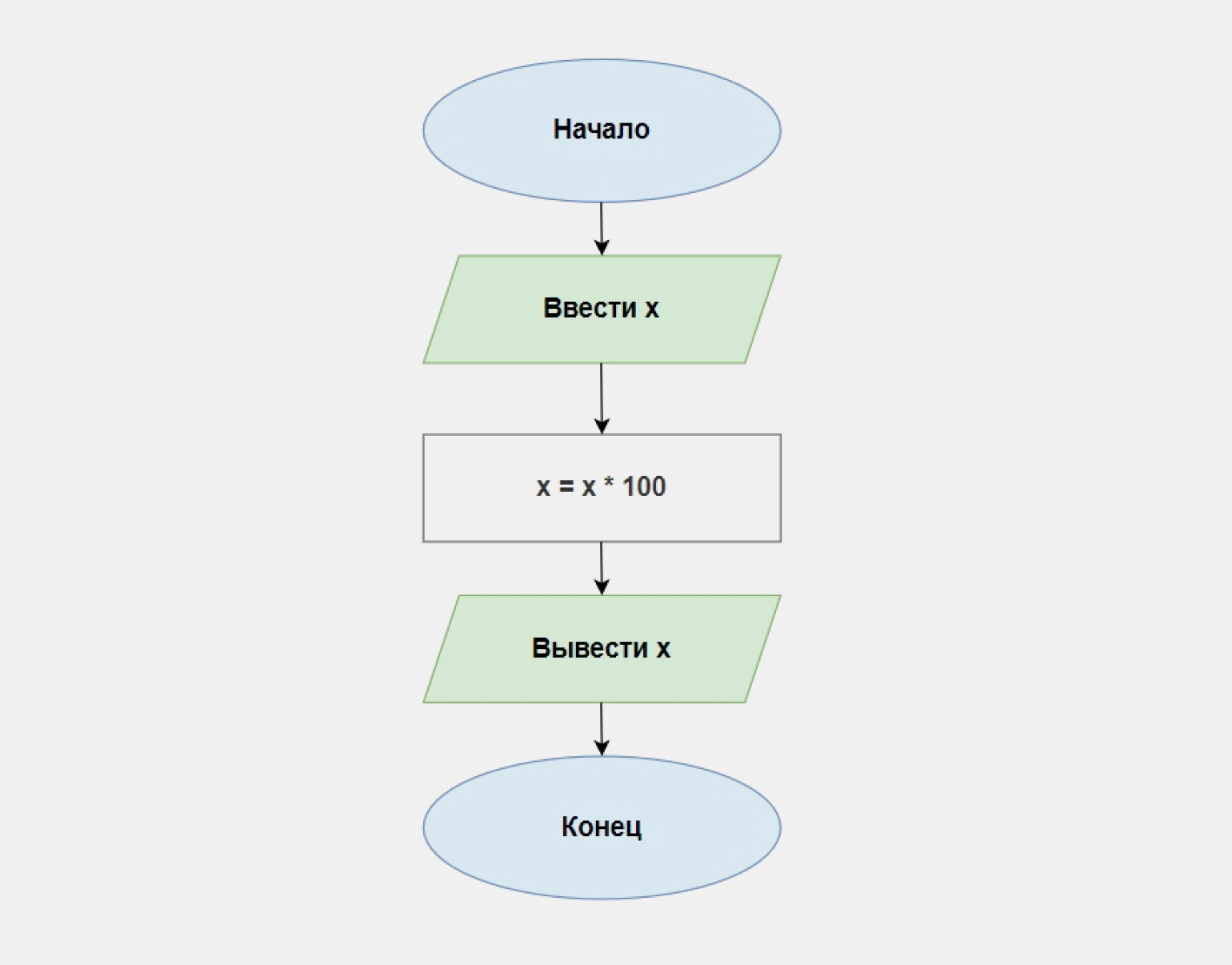
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
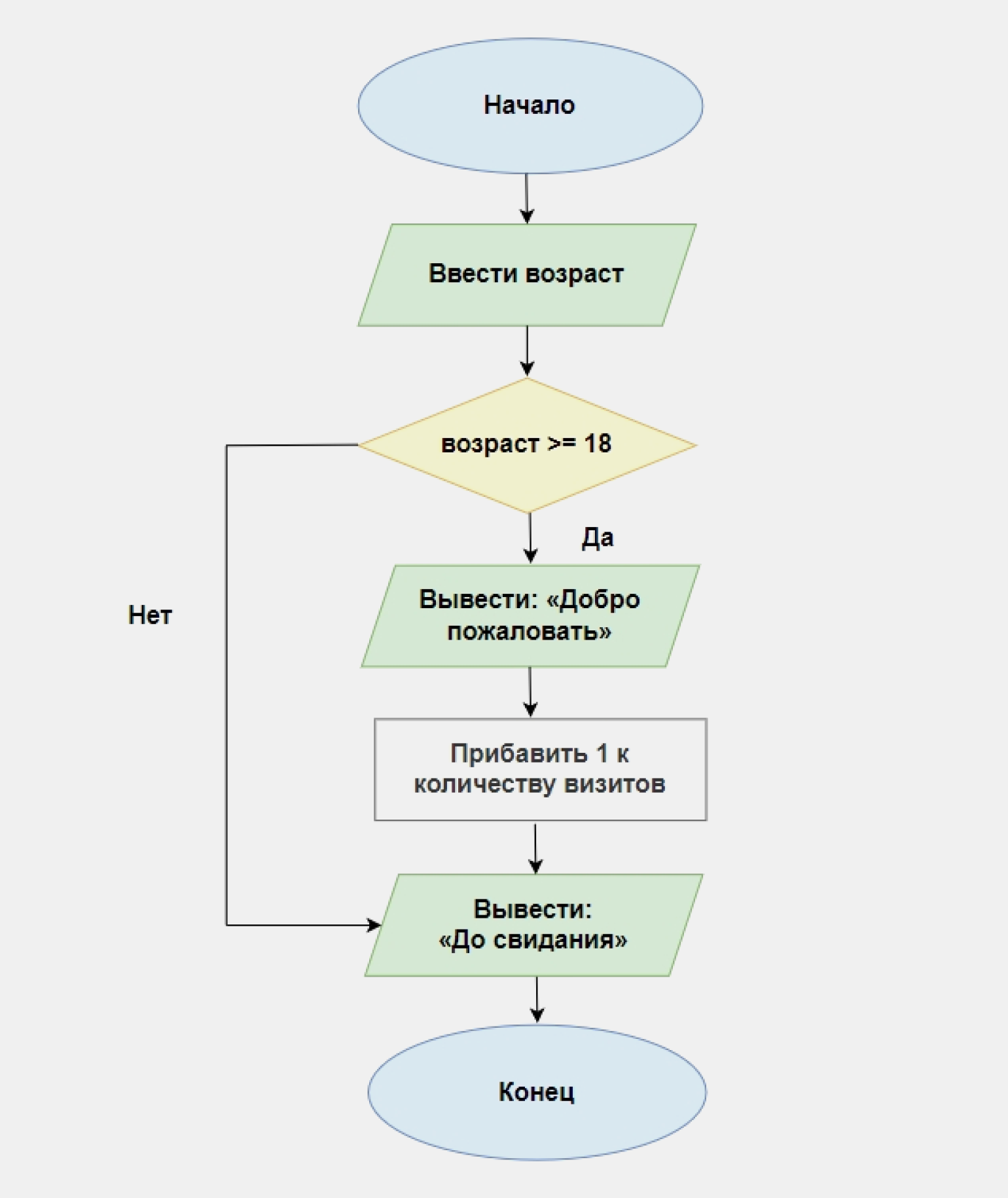
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
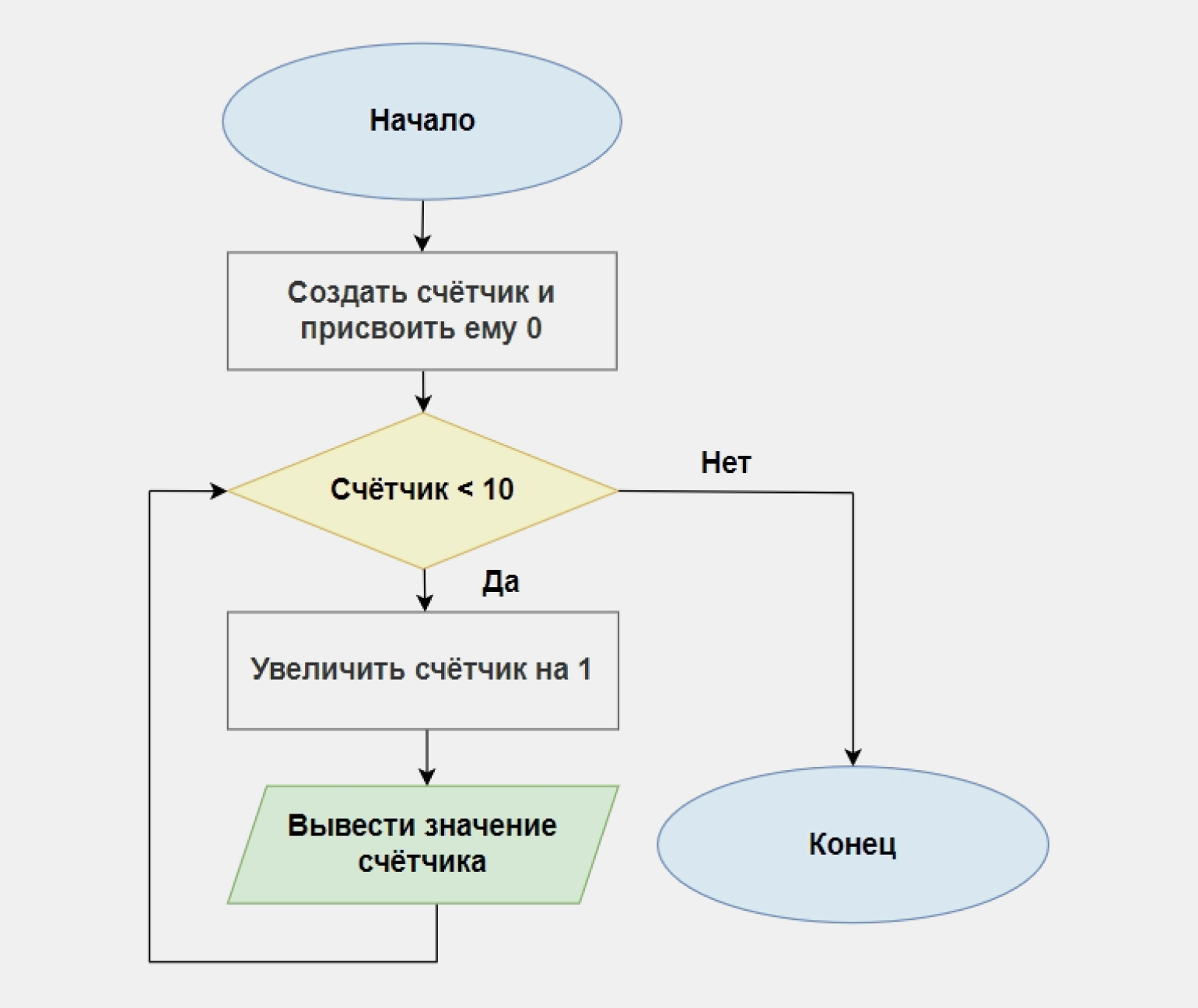
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
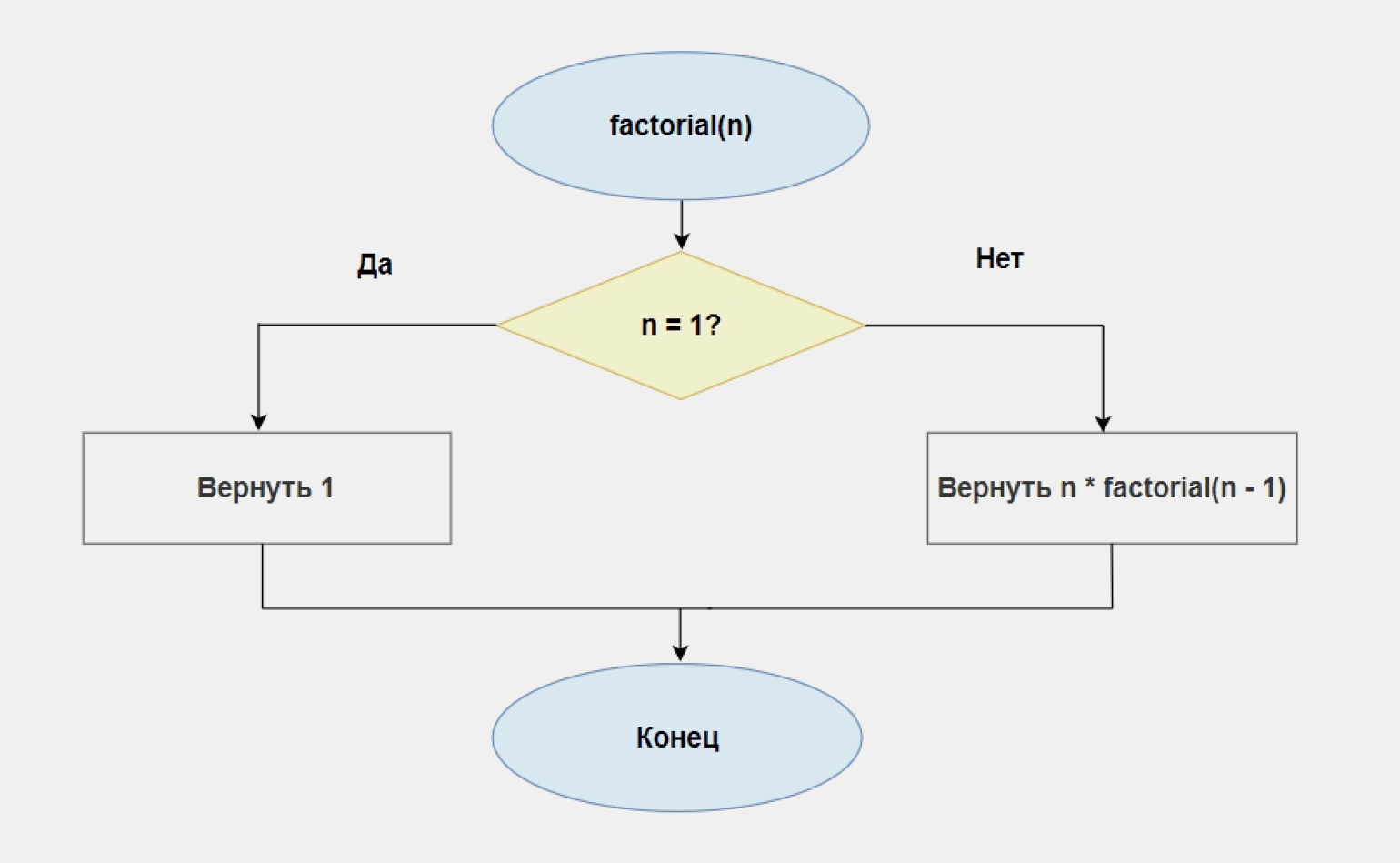
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Нейросети вам помогут.
Большой вебинар по нейросетям. 15 экспертов, 7 топ-нейросетей. Научитесь использовать ИИ в своей работе и повысьте эффективность.
Узнать больше
Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.
Ранее часто писали «алгорифм», сейчас такое написание используется редко, но, тем не менее, имеет место (например, Нормальный алгорифм Маркова).
Часто в качестве исполнителя выступает некоторый механизм (компьютер, токарный станок, швейная машина), но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек.
Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако, в явном виде понятие алгоритма сформировалось лишь в начале XX века.
Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений[1] или «эффективного метода»[2]; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга. В методологии алгоритм является базисным понятием и получает качественно новое понятие как оптимальности по мере приближения к прогнозируемому абсолюту. В современном мире алгоритм в формализованном выражении составляет основу образования на примерах, по подобию. На основе сходства алгоритмов различных сфер деятельности была сформирована концепция (теория) экспертных систем.
Содержание
- 1 История термина
- 2 Определения алгоритма
- 2.1 Формальное определение
- 2.1.1 Машина Тьюринга
- 2.1.2 Рекурсивные функции
- 2.1.3 Нормальный алгоритм Маркова
- 2.2 Стохастические алгоритмы
- 2.3 Другие формализации
- 2.1 Формальное определение
- 3 Формальные свойства алгоритмов
- 4 Виды алгоритмов
- 5 Нумерация алгоритмов
- 6 Алгоритмически неразрешимые задачи
- 7 Анализ алгоритмов
- 7.1 Время работы
- 8 Наличие исходных данных и некоторого результата
- 9 Представление алгоритмов
- 10 Эффективность алгоритмов
- 11 Пример
- 12 См. также
- 13 Примечания
- 14 Литература
- 15 Ссылки
История термина
Страница из «Алгебры» аль-Хорезми — хорезмского математика, от имени которого происходит слово алгоритм.
Современное формальное определение алгоритма было дано в 30—50-е годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.
Само слово «алгоритм» происходит от имени хорезмского учёного Абу Абдуллах Мухаммеда ибн Муса аль-Хорезми (алгоритм — аль-Хорезми). Около 825 года он написал сочинение, в котором впервые дал описание придуманной в Индии позиционной десятичной системы счисления. К сожалению, персидский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (её индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритмы о счёте индийском»). По-арабски же книга именовалась Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»). Из оригинального названия книги происходит слово Алгебра (алгебра — аль-джебр — восполнение).
Таким образом, мы видим, что латинизированное имя среднеазиатского учёного было вынесено в заглавие книги, и сегодня считается, что слово «алгоритм» попало в европейские языки именно благодаря этому сочинению. Однако вопрос о его смысле длительное время вызывал ожесточённые споры. На протяжении многих веков происхождению слова давались самые разные объяснения.
Одни выводили algorism из греческих algiros (больной) и arithmos (число). Из такого объяснения не очень ясно, почему числа именно «больные». Или же лингвистам больными казались люди, имеющие несчастье заниматься вычислениями? Своё объяснение предлагал и энциклопедический словарь Брокгауза и Ефрона. В нём алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень». Разумеется, эти объяснения вряд ли можно счесть убедительными.
Упомянутый выше перевод сочинения аль-Хорезми стал первой ласточкой, и в течение нескольких следующих столетий появилось множество других трудов, посвящённых всё тому же вопросу — обучению искусству счёта с помощью цифр. И все они в названии имели слово algoritmi или algorismi.
Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), всё ещё связывали это слово с именем конкретного человека. Очень распространённой была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:
Алгоризм был придуман в Греции. Это часть арифметики. Придуман он был мастером по имени Алгоризм, который дал ему своё имя. И поскольку его звали Алгоризм, Он назвал свою книгу «Алгоризм».
Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счёте мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.
«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счётного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюблённые. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счётчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.
Впрочем, греческая версия была не единственной. Мифический АлГор (Algor) именовался то королём Кастилии (Rex quodam Castelliae), то индийским королём, то арабским мудрецом (philosophus Algus nomine Arabicus), то египетским божеством. Соответственно АлГорРитм — это ритм (порядок) бога Гора (АлГора).
Баронесса Ада Лавлейс, которую считают первым программистом.
Однако со временем такие объяснения всё менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г.
Алгоритм — это искусство счёта с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчёмного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.
Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и учёные. Достоинства вычислений на счётной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счёта окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).
Итак, сочинения по искусству счёта назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).
Постепенно значение слова расширялось. Учёные начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошёл к идее логарифмов. Когда же на смену абаку пришёл так называемый счёт на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счёта на линиях.
Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.
В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.
В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus всё ещё объясняется как понятие о четырёх арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена ещё только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.
Однако потребовалось ещё почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.
Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счётная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к ещё более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по еллински и по гречески арифметика, а по немецки алгоризма, а по русски цифирная счётная мудрость».
Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырёх арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определённым правилам, и это объяснение также даётся в следующих изданиях БСЭ.
Алгоритмы становились предметом всё более пристального внимания учёных, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далёких, то к началу сороковых годов это слово они могли услышать разве что во время учёбы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм всё ещё воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объёмных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.
Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров. Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они ещё не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далёкого будущего. Соответственно и алгоритмы ни разу не упоминаются на её страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ». За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится всё более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живёт, обогащаясь всё новыми значениями и смысловыми оттенками.
Определения алгоритма
Формальное определение
Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.
Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Чёрча — Тьюринга)[3]
Машина Тьюринга
Схематическая иллюстрация работы машины Тьюринга.
Основная идея, лежащая в основе машины Тьюринга, очень проста. Машина Тьюринга — это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шагу машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом, машина может изменить свое состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево.[4]
На основе исследования этих машин был выдвинут тезис Тьюринга (основная гипотеза алгоритмов):
Этот тезис является аксиомой, постулатом, и не может быть доказан математическими методами, поскольку алгоритм не является точным математическим понятием.
Рекурсивные функции
С каждым алгоритмом можно сопоставить функцию, которую он вычисляет. Однако возникает вопрос, можно ли произвольной функции сопоставить машину Тьюринга, а если нет, то для каких функций существует алгоритм? Исследования этих вопросов привели к созданию в 1930-х годах теории рекурсивных функций[5].
Класс вычислимых функций был записан в образ, напоминающий построение некоторой аксиоматической теории на базе системы аксиом. Сначала были выбраны простейшие функции, вычисление которых очевидно. Затем были сформулированы правила (операторы) построения новых функций на основе уже существующих. Необходимый класс функций состоит из всех функций, которые можно получить из простейших применением операторов.
Подобно тезису Тьюринга в теории вычислительных функций была выдвинута гипотеза, которая называется тезис Чёрча:
Доказательство того, что класс вычислимых функций совпадает с исчисляемыми по Тьюрингу, происходит в два шага: сначала доказывают вычисление простейших функций на машине Тьюринга, а затем — вычисление функций, полученных в результате применения операторов.
Таким образом, неформально алгоритм можно определить как четкую систему инструкций, определяющих дискретный детерминированный процесс, который ведет от начальных данных (на входе) к искомому результату (на выходе), если он существует, за конечное число шагов; если искомого результата не существует, алгоритм или никогда не завершает работу, либо заходит в тупик.
Нормальный алгоритм Маркова
Нормальный алгоритм Маркова — это система последовательных применений подстановок, которые реализуют определенные процедуры получения новых слов из базовых, построенных из символов некоторого алфавита. Как и машина Тьюринга, нормальные алгоритмы не выполняют самих вычислений: они лишь выполняют преобразование слов путем замены букв по заданным правилам[6].
Нормально вычислимой называют функцию, которую можно реализовать нормальным алгоритмом. То есть, алгоритмом, который каждое слово из множества допустимых данных функции превращает в ее исходные значения[7]..
Создатель теории нормальных алгоритмов А. А. Марков выдвинул гипотезу, которая получила название принцип нормализации Маркова:
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не может быть доказан математическими средствами.
Стохастические алгоритмы
Однако, приведенное выше формальное определение алгоритма в некоторых случаях может быть слишком строгим. Иногда возникает потребность в использовании случайных величин[8]. Алгоритм, работа которого определяется не только исходными данными, но и значениями, полученными из генератора случайных чисел, называют стохастическим (или рандомизированным, от англ. randomized algorithm)[9]. Формально, такие алгоритмы нельзя называть алгоритмами, поскольку существует вероятность (близкая к нулю), что они не остановятся. Однако, стохастические алгоритмы часто бывают эффективнее детерминированных, а в отдельных случаях — единственным способом решить задачу[8].
На практике вместо генератора случайных чисел используют генератор псевдослучайных чисел.
Однако следует отличать стохастические алгоритмы и методы, которые дают с высокой вероятностью правильный результат. В отличие от метода, алгоритм дает корректные результаты даже после продолжительной работы.
Некоторые исследователи допускают возможность того, что стохастический алгоритм даст с некоторой заранее известной вероятностью неправильный результат. Тогда стохастические алгоритмы можно разделить на два типа[10]:
- алгоритмы типа Лас-Вегас всегда дают корректный результат, но время их работы не определено.
- алгоритмы типа Монте-Карло, в отличие от предыдущих, могут давать неправильные результаты с известной вероятностью (их часто называют методами Монте-Карло).
Другие формализации
Для некоторых задач названные выше формализации могут затруднять поиск решений и осуществление исследований. Для преодоления препятствий были разработаны как модификации «классических» схем, так и созданы новые модели алгоритма. В частности, можно назвать:
- многоленточная и недетерминированная машины Тьюринга;
- регистровая и РАМ машина — прототип современных компьютеров и виртуальных машин;
- конечные и клеточные автоматы
и другие.
Формальные свойства алгоритмов
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
- Дискретность — алгоритм должен представлять процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.
- Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа. Однако при включении метода генерации случайных чисел в список «исходных данных», вероятностный алгоритм становится подвидом обычного.
- Понятность — алгоритм должен включать только те команды, которые доступны исполнителю и входят в его систему команд.
- Завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов.[источник не указан 713 дней] С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.
- Массовость (универсальность). Алгоритм должен быть применим к разным наборам исходных данных.
- Результативность — завершение алгоритма определёнными результатами.
- Алгоритм содержит ошибки, если приводит к получению неправильных результатов либо не даёт результатов вовсе.
- Алгоритм не содержит ошибок, если он даёт правильные результаты для любых допустимых исходных данных.
Виды алгоритмов
Особую роль выполняют прикладные алгоритмы, предназначенные для решения определённых прикладных задач. Алгоритм считается правильным, если он отвечает требованиям задачи (например, даёт физически правдоподобный результат). Алгоритм (программа) содержит ошибки, если для некоторых исходных данных он даёт неправильные результаты, сбои, отказы или не даёт никаких результатов вообще. Последний тезис используется в олимпиадах по алгоритмическому программированию, чтобы оценить составленные участниками программы.
Важную роль играют рекурсивные алгоритмы (алгоритмы, вызывающие сами себя до тех пор, пока не будет достигнуто некоторое условие возвращения). Начиная с конца XX — начала XXI века активно разрабатываются параллельные алгоритмы, предназначенные для вычислительных машин, способных выполнять несколько операций одновременно.
Нумерация алгоритмов
Нумерация алгоритмов играет важную роль в их исследовании и анализе[11]. Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счётное, то множество всех алгоритмов также счётное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.
Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.
Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.
Алгоритмически неразрешимые задачи
Формализация понятия алгоритма позволила исследовать существование задач, для которых не существует алгоритмов поиска решений. Впоследствии была доказана невозможность алгоритмического вычисления решений ряда задач, что делает невозможным их решение на любом вычислительном устройстве. Функцию 


Случай, когда результатом вычисления функции 

Важно точно указывать допустимое множество входных данных, поскольку задача может быть решаемой для одного множества и нерешаемой для другого.
Одной из первых задач, для которой была доказана нерешаемость, является проблема остановки. Формулируется она следующим образом:
Доказательство неразрешимости проблемы остановки важно тем, что к ней можно свести другие задачи. Например, простую проблему остановки можно свести к задаче остановки на пустой строке (когда нужно определить для заданной машины Тьюринга, остановится ли она, будучи запущенной на пустой строке), доказав тем самым неразрешимость последней. [12].
Анализ алгоритмов
Вместе с распространением информационных технологий увеличился риск программных сбоев. Одним из способов избежания ошибок в алгоритмах и их реализациях служат доказательства корректности систем математическими средствами.
Использование математического аппарата для анализа алгоритмов и их реализаций называют формальными методами. Формальные методы предусматривают применение формальных спецификаций и, обычно, набора инструментов для синтаксического анализа и доказательства свойств спецификаций. Абстрагирование от деталей реализации позволяет установить свойства системы независимо от ее реализации. Кроме того, точность и однозначность математических утверждений позволяет избежать многозначности и неточности естественных языков[14].
По гипотезе Ричарда Мейса, «избежание ошибок лучше устранения ошибок»[15]. По гипотезе Хоара, «доказательство программ решает проблему корректности, документации и совместимости»[16]. Доказательство корректности программ позволяет выявлять их свойства по отношению ко всему диапазону входных данных. Для этого понятие корректности было разделено на два типа:
- Частичная корректность — программа дает правильный результат для тех случаев, когда она завершается.
- Полная корректность — программа завершает работу и выдает правильный результат для всех элементов из диапазона входных данных.
Во время доказательства корректности сравнивают текст программы со спецификацией желаемого соотношения входных-выходных данных. Для доказательств типа Хоара эта спецификация имеет вид утверждений, которые называют предусловиями и постусловиями. В совокупности с самой программой, их еще называют тройкой Хоара. Эти утверждения записывают
- P{Q}R
где P — это предусловие, что должно выполняться перед запуском программы Q, а R — постусловие, правильное после завершения работы программы.
Формальные методы были успешно применены для широкого круга задач, в частности: разработке электронных схем, искусственного интеллекта, автоматических систем на железной дороге, верификации микропроцессоров, спецификации стандартов и спецификации и верификации программ[17].
Время работы
Графики функций, приведенных в таблице ниже.
Распространенным критерием оценки алгоритмов является время работы и порядок роста продолжительности работы в зависимости от объема входных данных.[18]
Для каждой конкретной задачи составляют некоторое число, которое называют ее размером. Например, размером задачи вычисления произведения матриц может быть наибольший размер матриц-множителей, для задач на графах размером может быть количество ребер графа.
Время, которое тратит алгоритм как функция от размера задачи 
Именно асимптотическая сложность определяет размер задач, которые алгоритм способен обработать. Например, если алгоритм обрабатывает входные данные размером 
Часто, во время разработки алгоритма пытаются уменьшить асимптотическую временную сложность для наихудших случаев. На практике же бывают случаи, когда достаточным является алгоритм, который «обычно» работает быстро.
Грубо говоря, анализ средней асимптотической временной сложности можно разделить на два типа: аналитический и статистический. Аналитический метод дает более точные результаты, но сложен в использовании на практике. Зато статистический метод позволяет быстрее осуществлять анализ сложных задач[19].
В следующей таблице приведены распространенные асимптотические сложности с комментариями[20].
| Сложность | Комментарий | Примеры |
|---|---|---|
| O(1) | Устойчивое время работы не зависит от размера задачи | Ожидаемое время поиска в в хеш-таблице |
| O(log log n) | Очень медленный рост необходимого времени | Ожидаемое время работы интерполирующего поиска n элементов |
| O(log n) | Логарифмический рост — удвоение размера задачи увеличивает время работы на постоянную величину | Вычисление xn; Двоичный поиск в массиве из n элементов |
| O(n) | Линейный рост — удвоение размера задачи удвоит и необходимое время | Сложение/вычитание чисел из n цифр; Линейный поиск в массиве из n элементов |
| O(n log n) | Линеаритмичный рост — удвоение размера задачи увеличит необходимое время чуть более чем вдвое | Сортировка слиянием или кучей n элементов; нижняя граница сортировки сопоставлением n элементов |
| O(n²) | Квадратичный рост — удвоение размера задачи увеличивает необходимое время в четыре раза | Элементарные алгоритмы сортировки |
| O(n³) | Кубичный рост — удвоение размера задачи увеличивает необходимое время в восемь раз | Обычное умножение матриц |
| O(cn) | Экспоненциальный рост — увеличение размера задачи на 1 приводит к c-кратному увеличению необходимого времени; удвоение размера задачи увеличивает необходимое время в квадрат | Некоторые задачи коммивояжёра, алгоритмы поиска полным перебором |
Наличие исходных данных и некоторого результата
Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание, исполнительно совершить последовательность действий, направленных на достижение цели.
Представление алгоритмов
Формы записи алгоритма:
- словесная или вербальная (языковая, формульно-словесная);
- дракон-схема;
- псевдокод (формальные алгоритмические языки);
- схематическая:
- структурограммы (схемы Насси-Шнайдермана);
- графическая (блок-схемы).
Обычно сначала (на уровне идеи) алгоритм описывается словами, но по мере приближения к реализации он обретает всё более формальные очертания и формулировку на языке, понятном исполнителю (например, машинный код).
Эффективность алгоритмов
Хотя в определении алгоритма требуется лишь конечность числа шагов, требуемых для достижения результата, на практике выполнение даже хотя бы миллиарда шагов является слишком медленным. Также обычно есть другие ограничения (на размер программы, на допустимые действия). В связи с этим вводят такие понятия как сложность алгоритма (временна́я, по размеру программы, вычислительная и др.).
Для каждой задачи может существовать множество алгоритмов, приводящих к цели. Увеличение эффективности алгоритмов составляет одну из задач современной информатики. В 50-х гг. XX века появилась даже отдельная её область — быстрые алгоритмы. В частности, в известной всем с детства задаче об умножении десятичных чисел обнаружился ряд алгоритмов, позволяющих существенно (в асимптотическом смысле) ускорить нахождение произведения. См. быстрое умножение
Ярким примером является алгоритм Чудновского для вычисления числа 
Пример
В качестве примера можно привести алгоритм Евклида.
Алгоритм Евклида — эффективный метод вычисления наибольшего общего делителя (НОД). Назван в честь греческого математика Евклида; один из древнейших алгоритмов, который используют до сих пор[21].
Описан в «Началах» Евклида (примерно 300 до н. э.), а именно в книгах VII и X. В седьмой книге описан алгоритм для целых чисел, а в десятой — для длин отрезков.
Существует несколько вариантов алгоритма, ниже записанный в псевдокоде рекурсивный вариант:
функция нод(a, b)
если b = 0
возврат a
иначе
возврат нод(b, a mod b)
Иллюстрация выполнения алгоритма Евклида для вычисления НОД чисел 1599 и 650.
НОД чисел 1599 и 650:
| Шаг 1 | 1599 = 650*2 + 299 |
| Шаг 2 | 650 = 299*2 + 52 |
| Шаг 3 | 299 = 52*5 + 39 |
| Шаг 4 | 52 = 39*1 + 13 |
| Шаг 5 | 39 = 13*3 + 0 |
См. также
- Список алгоритмов
- Адаптивный алгоритм
- Метаалгоритм
- Теория алгоритмов
Примечания
- ↑ Kleene 1943 in Davis 1965:274
- ↑ Rosser 1939 in Davis 1965:225
- ↑ (Игошин, с. 317)
- ↑ Basics: The Turing Machine (with an interpreter!. Good Math, Bad Math (9 февраля 2007). Архивировано из первоисточника 2 февраля 2012.
- ↑ (Игошин, раздел 33)
- ↑ Энциклопедия кибернетики, т. 2, c. 90-91.
- ↑ (Игошин, раздел 34)
- ↑ 1 2 «Probabilistic algorithms should not be mistaken with methods (which I refuse to call algorithms), which produce a result which has a high probability of being correct. It is essential that an algorithm produces correct results (discounting human or computer errors), even if this happens after a very long time.» Henri Cohen A Course in Computational Algebraic Number Theory. — Springer-Verlag, 1996. — P. 2. — ISBN 3-540-55640-0
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rives’t, Clifford Stein . — ISBN 0-262-03293-7
- ↑ (Раздел 12, с. 12-22 в Atallah, 2010)
- ↑ (Игошин, раздел 36)
- ↑ 1 2 3 Peter Linz An Introduction to Formal Languages and Automata. — Jones and Bartlett Publishers, 2000. — ISBN 0-7637-1422-4
- ↑ «computability and complexity», Encyclopedia of computer Science and Technology, Facts On File, 2009, ISBN 978-0-8160-6382-6
- ↑ (O’Regan, раздел 4.5)
- ↑ (раздел 5.3.6 в Enders, 2003)
- ↑ (раздел 5.3.7 в Enders, 2003)
- ↑ (O’Regan, с. 119)
- ↑ А. Ахо, Дж. Хопкрофт, Дж. Ульман Построение и анализ вычислительных алгоритмов = The Design and Analysis of Computer Algorithms. — «Мир», 1979.
- ↑ (раздел 11 в Atallah, 2010)
- ↑ (раздел 1 в Atallah, 2010)
- ↑ Knuth D The Art of Computer Programming, Volume 2: Seminumerical Algorithms. — 3rd. — Addison–Wesley, 1997. — ISBN 0201896842
Литература
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Порублев Илья Николаевич, Ставровский Андрей Борисович. Алгоритмы и программы. Решение олимпиадных задач. — М.: «Вильямс», 2007. — С. 480. — ISBN 978-5-8459-1244-2
- Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стер.. — М.: ИЦ «Академия», 2008. — 448 с. — ISBN 5-7695-1363-2
Ссылки
| алгоритм в Викисловаре? | |
| Что такое алгоритм в Викиучебнике? |
- «Слово „алгоритм“: происхождение и развитие», В. В. Шилов, Журнал «Потенциал» — источник исторических сведений.
- Алгоритмы, методы, исходники — сайт по алгоритмам и методам программирования
- Дискретная математика: Алгоритмы — список алгоритмов
- Юрий Лифшиц. Курс лекций Алгоритмы для Интернета
- Геометрические алгоритмы
- об алгоритме в энциклопедии «Кругосвет»
- Сборник алгоритмов на сайте e-maxx.ru