Оригами многогранники из бумаги пошаговая инструкция

Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.

Ажурная модель

Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.

Пошаговая инструкция:

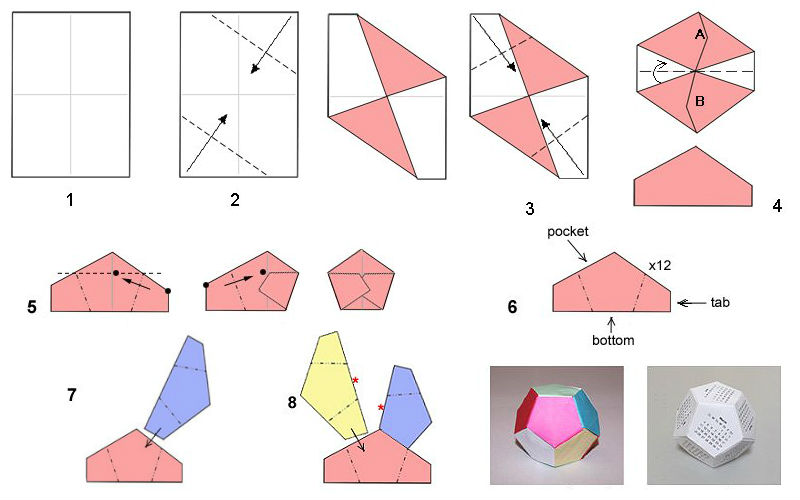
1. Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
2. Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
3. Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
4. Складываем фигуру по диагонали, как показано на рис 4.
5. Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

Пошаговая инструкция:

1. Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
2. Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
3. Аналогично складываем противоположные углы.
4. Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
5. Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
6. Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
7. Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
8. Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Додекаэдр-звезда

Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.

Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.

Интересные факты о додекаэдре

Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.

Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.

Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.

Игрушки древних римлян

На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.

В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.

Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.

Как сделать модель тетраэдра из бумаги и картона

Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.

Традиционный вариант

Объёмный тетраэдр-оригами можно сделать из классического квадрата или листа бумаги формата А4. Схема во втором варианте – сложнее, однако для долговечного декора лучше выбирать именно её. Модель получается многослойной, а потому меньше изнашивается в процессе эксплуатации.

Пошаговая инструкция:

Нам понадобится 2 альбомных листа. Складываем их поочерёдно по одному и тому же алгоритму.

1. Располагаем лист короткой стороной к себе. Намечаем вертикальную ось симметрии.
2. Правый нижний угол поднимаем к центральной линии из шага 1.
3. Переворачиваем заготовку.
4. Левый верхний угол опускаем, делая сгиб по линии, намеченной в шаге 2.
5. Вот что должно получиться.
6. Раскрываем изделие.
7. Повторяем шаги 2-5 с другой стороны.
8. Срезаем верхнюю часть по выделенной на схеме линии.

1. Складываем левый верхний угол по пунктиру. Его вершину совмещаем с точкой, указанной стрелкой.
2. Повторяем то же действие для правого нижнего угла.
3. Вот такая полоска-«конверт» должна получиться.
4. Повторяем шаги 1-10 для другого листа А4, но зеркально.
5. Кладём один модуль поверх другого, как показано на схеме.
6. Нижний элемент складываем в тетраэдр.
7. Оборачиваем верхнюю часть вокруг получившейся фигуры.
8. Вставляем оставшийся клапан в зазор, чтобы тетраэдр-оригами не распадался.

Эта модель великолепно смотрится в настенных панно:

Есть и немного другая схема сборки тетраэдра – из одного листа А4. Она представлена в видео-уроке:

Модель от Томоко Касахары

Японский оригамист предлагает сделать модель тетраэдра из квадратного листа. Схема сборки от Касахары настолько подробная, что изготовить по ней фигурку сможет даже начинающий. Для удобства рекомендуется использовать бумагу со сторонами разного цвета – это поможет следить за процессом складывания. Опытные мастера могут брать однотонные листы, что улучшит эстетические качества модели.

Пошаговая инструкция:

1. Начинаем с изнанки листа. Делим квадрат пополам путём складывания. Намечаем «засечку» и раскрываем сгиб. Правую половину тоже складываем вдвое. Наносим отметку примерно на полпути вверх. Разворачиваем лист до исходного состояния.
2. Делаем сгиб по пунктиру, ориентируясь на «засечки» из шага 1.
3. Повторяем аналогичное действие с противоположной стороны.
4. Опускаем верхний край на 1 см.
5. Подгибаем уголки по стрелкам.
6. Раскрываем все складки, кроме последних. Делим новый квадрат пополам по горизонтали.

1. Намечаем диагональные сладки в местах, указанных пунктиром.
2. Делаем короткие боковые сгибы по стрелкам. Важно каждый раз совмещать нижний край клапана с меткой по центру.
3. Предварительные сгибы нанесены, теперь можно переходить к складыванию объёмной фигуры. Нижний левый угол сгибаем по пунктирной линии до пересечения, указанного стрелкой.
4. Далее совмещаем его с вершиной треугольника.
5. Точку 1 опускаем до конца стрелки, а затем откидываем клапан 2, чтобы зафиксировать последний сгиб.
6. Получившаяся фигура напоминает перевёрнутый рожок для мороженого. Нажимаем на складки в правой части модели, поднимаем точку 1 вверх, как показано на схеме, и «заправляем» под клапан. Тетраэдр-оригами почти готов, но у него остаётся одна лишняя грань. Чтобы завершить сборку, точку 2 перемещаем по стрелке и фиксируем клапаном.

Освоив схему сборки тетраэдра Касахары, можно также изготавливать из бумаги своими руками эффектные подарки – разнообразные панно и картины:

Альтернативный вариант сборки из квадрата:

Очень простая двухцветная модель

Необычно и эффектно смотрится тетраэдр из двух половинок. Каждую можно сложить из бумаги другого цвета, что сделает геометрический декор ещё интереснее. Если предыдущие модели адресованы, скорее, опытным мастерам, эта – как раз по плечу начинающим.

Пошаговая инструкция:

1. Сгибаем квадрат по диагонали «горой». Делим пополам, складывая слева направо и сверху вниз. Делаем складки и раскрываем.
2. Намечаем сгиб слева по пунктирной линии. Соединяем вершину угла с ближней засечкой.
3. Аналогичные сгибы делаем ещё с трёх сторон.
4. Все четыре края складываем по пунктирным линиям. Центральные треугольники выступают вверх, образуя так называемые «заячьи уши». Раскрываем их изнутри и сплющиваем.
5. Сгибаем фигуру пополам «долиной».

Аналогичным образом собираем вторую часть. Остаётся склеить двухцветный тетраэдр из бумаги и придумать ему применение.

Декор из картона

Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:

Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:

Звёздчатый многогранник

Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.

Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.

Пошаговая инструкция:

Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.

1. Первую полосу сгибаем вдвое по высоте. Раскрываем складку.
2. Оба края сводим к середине.
3. Делаем складку-засечку «долиной».
4. Левый угол сгибаем, чтобы красная точка коснулась отметки из шага 3. Раскрываем.
5. С помощью обратной складки заводим левый угол внутрь.
6. Раскрываем правую сторону. «Прячем» выступающий уголок. И вновь закрываем правую половину.
7. Намечаем складку «долиной» с другой стороны.
8. Повторяем шаги 3-7 на противоположном конце полосы.

Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».

Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.

Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.

К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.

Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.

Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.

Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.

Последний, фиолетовый, многоугольник крепим с особой тщательностью.

Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.

Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.

Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.

А эксцентричные невесты вполне могут заменить им свадебный букет.

Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:

Интересные факты

Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.

Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.

В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.

Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.

Источник

Как сделать многогранник из бумаги

Когда-то разноцветные многогранники из бумаги и картона служили одновременно и наглядным пособием, и украшением школьных кабинетов математики и черчения. Изготовление этих фигур способствовало развитию пространственного мышления, знакомило с многообразием форм в их трехмерном проявлении. Изготовление таких многогранников из цветной бумаги — увлекательнейшее занятие, не лишенное интеллектуальной составляющей, удивительная возможность математикой выразить красоту окружающего мира.

Многогранник — понятие очень обширное, и зачастую новички, увлеченные изготовлением этих выпуклых и звездчатых фигур, поначалу путаются в их названиях, что, в общем-то, неудивительно. Многогранники можно разделить на две категории: так называемые Платоновы тела и Архимедовы тела.

К первым относятся правильные многогранники: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр. Ко вторым — полуправильные многогранники: усеченные версии Платоновых тел, кубооктаэдр, «курносый» куб и др. Не старайтесь сразу запомнить все эти сложные названия, мастерить их гораздо интереснее, чем заучивать термины 🙂

Для работы понадобится цветной или белый картон, который можно при необходимости раскрасить; линейка и угольники; хороший клей, который не коробит бумагу; ножницы; пинцет. Для изготовления заготовок многогранника удобно пользоваться картонными трафаретами: чертеж заготовки накладывают на плотный картон, шилом или иголкой делают проколы по вершинам детали, после чего по линейке соединяют эти точки.

Тетраэдр

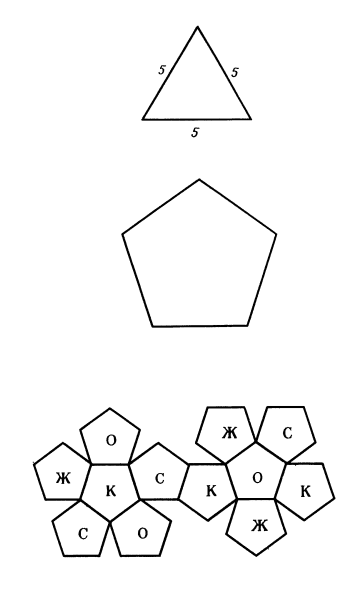
Одним из простейших многогранников, которые проще всего сделать из бумаги (картона), является тетраэдр («Пирамида»). Четыре грани этой фигуры представлены равносторонними треугольниками. Если хочется сделать одноцветный тетраэдр, то можно воспользоваться одной разверткой (см. схему ниже).

Если же тетраэдр нужен разноцветный, то придется сделать четыре цветные заготовки в виде равносторонних прямоугольников. Из картона изготавливают четыре треугольника разного цвета (например, Ж, С, О, К — желтый, синий, оранжевый, красный), обязательно делая небольшие «припуски» для склеивания деталей.

При соединении отдельных заготовок сначала склеивают все четыре детали в положение, изображенное на рисунке ниже, затем приступают к соединению боковых граней. Сначала склеивают между собой только две из них, затем — оставшиеся детали.

Октаэдр

Вторую половину проще клеить таким образом: сначала четыре оставшихся треугольника приклеивают к соответствующим сторонам квадратного основания, затем соединяют соседние грани.

Икосаэдр

На третьем месте по простоте исполнения идет икосаэдр, гранями которого тоже являются равносторонние треугольники. Наиболее эффектно смотрятся разноцветные многогранники, у которых возможно варьирование распределения цветов. Например, можно сделать фигуру, у которой в каждой вершине будут сходиться все используемые цвета, или же у противоположных граней будут одинаковые расцветки, а у вершин будет повторяться один цвет.

Модель собирают из пяти треугольников, соединенных по схеме, указанной на рисунке ниже. В результате получится невысокая пятиугольная пирамида без основания. К сторонам основания приклеивают остальные пять треугольников, руководствуясь любой понравившейся цветовой схемой.

Додекаэдр

И, пожалуй, к несложным, но самым эффектным по своему внешнему виду многогранникам можно отнести додекаэдр. Наиболее красиво выглядят разноцветные додекаэдры: четырех- или шестицветные.

Построение модели начинают со приклеивания пяти разноцветных пятиугольников к центральному пятиугольнику — например, белого цвета. Затем цветные заготовки склеивают между собой — получается половина додекаэдра. Затем остальные грани заготовок подклеивают к уже готовой половине фигуры таким образом, чтобы выдержать задуманную цветовую схему и эффектный многогранник из бумаги будет готов.

Если вам, уважаемые читатели, интересна тема изготовления многогранников из бумаги, и хотелось бы видеть больше схем, пишите об этом в комментариях, публикации будут продолжены. Впереди нас ждут усеченные, «курносые» и красивейшие звездчатые формы многогранников.

Источник

Мастер-класс

«Технология
изготовления многогранников с помощью оригами»

Разработчик:
Чернакова Ирина Львовна – преподаватель математики
ГАПОУ АО «Архангельский политехнический техникум»        (слайд
1)

Целевая
аудитория: мастер-класс «Технология изготовления многогранников с помощью
оригами» проводится для преподавателей математики.

Время
проведения: 30 минут.                                                 

Цель
мастер-класса: познакомить аудиторию  с одной из форм
внеурочной деятельности    (слайд 2)

Задачи:

•      Познакомить
с  историей происхождения оригами, видами оригами;

•      Показать
связь математики и оригами на примере модульного оригами;

•      Познакомить
со схемами сборки многогранников  с помощью модулей;

•      Составить
модель куба с помощью оригами.

(слайд 3)

Оригами
— удивительное искусство бумажной пластики.

Японская
мудрость издревле гласит:
«Великий квадрат не имеет пределов».
Попробуй простую фигурку сложить,
И вмиг увлечёт интересное дело.

Сегодня множество людей во всем мире увлекаются искусством
«оригами». И каждый человек хоть раз в жизни создавал
самое простенькое изделие из квадратного листа бумаги —  кораблик, самолетик
или пилотку.

В последнее время обучающиеся всё с
большей неохотой относятся к учебе, и в частности к математике. Чтобы привлечь
их внимание к математике я решила показать им, что математика интересная,
творческая наука и при
помощи оригами из листа обычной бумаги можно не только творить самые невероятные
вещи, но и делать различные геометрические фигуры.
Мастера оригами говорят, что при складывании фигурок «голова работает руками».

История
происхождения оригами  (слайд 4)

Оригами в переводе с японского означает
«сложенная бумага».  «Ori» — это складывать, a
«kami» — бумага. Таким образом, оригами — это
древнее искусство складывания фигурок из бумаги.

История
возникновения оригами неразрывно связана с изобретением бумаги. Человечество за
время своего развития изобрело много различных материалов для письма. Это
папирус, глиняные таблички, береста, бамбуковые планки, пергамент и только в
начале первого тысячелетия в Китае изобрели бумагу. Китайцы изготавливали
бумагу из бамбуковых стеблей. Скоро секрет изготовления бумаги стал известен в
Японии. Японцы улучшили технологию производства и стали получать бумагу прочнее
и качественнее китайской. Лучшую бумагу в Японии делали из коры шелковичного
дерева. Такая бумага уже обладала свойствами необходимыми для складывания из
нее фигурок.

      Первые листочки бумаги, сложенные в необычные фигурки, появляются
сначала в монастырях. Фигурки из бумаги имели символическое значение. Ими
украшали храмы, они участвовали в религиозных церемониях, их помещали на жертвенный
костер.

(слайд 5)  
История оригами сохранила первые бумажные фигурки – коробочки
«санбо», куда японцы складывали кусочки овощей и рыбы для жертвоприношений.

    Со
временем оригами стало придворным искусством. Им могли заниматься лишь
избранные, так как бумага была редким и весьма дорогим материалом. Японцы
использовали бумажные фигурки для того, чтобы передать то или иное послание
другому человеку. Например, записки, сложенные в форме бабочки, журавля или
цветка, были символом дружбы и доброго пожелания. Только человек, владеющий
искусством оригами, может аккуратно развернуть и прочитать послание, не
предназначенное для посторонних глаз. В те времена умение богатого дворянина
развлечь свою даму на балу складыванием фигурок из бумажного листа считалось
признаком хорошего воспитания. Различные знатные семьи использовали фигурки оригами как герб и
печать.                  Далее бумага перестает быть предметом роскоши, и
оригами начинает распространяться и среди простого народа. Именно тогда, триста
– четыреста лет назад, изобретается ряд фигур, которым суждено было стать
классическими  (слайд 6). Среди них и японский журавлик «цуру» – традиционный японский
символ счастья и долголетия, а теперь и международный символ свободы и мира.

    (слайд
7)  Новый поворот в истории
оригами тесно связан со страшной трагедией, произошедшей 6 августа 1945 года,
когда была сброшена атомная бомба на Хиросиму. Последствия
чудовищного эксперимента были ужасны. Каждый, кто брался за оригами, знает
историю Садако,  девочки из Хиросимы, которая делала журавликов, веря, что это
спасёт её от лучевой болезни. Кто-то сказал ей, что, если она сделает 1000
журавликов, она поправится. Садако
скоро поняла, что ей уже не станет лучше, она умрёт. И тогда она стала дарить
журавликов другим больным. Каждый журавлик, которого делала Садако, был
молитвой, молитвой о спасении человека. Печальная история японской девочки
подняла волну детской солидарности во всём мире. Так
возникло движение «1000 журавликов».     

(слайд Новый
этап в развитии оригами начался после второй мировой войны и связан с именем
знаменитого японского мастера Йошизава Акира. Он
начал активно использовать оригами, объясняя с помощью складывания азы
геометрических понятий. А
так же  доказал, что искусство складывания может быть авторским.

      В настоящий момент оригами превратилось по-настоящему в
международное искусство. Сейчас центры оригами открыты в 26 государствах
планеты. Оригами развивается, во многих странах созданы общества оригамистов,
каждый год проводятся выставки и конференции.

     В России Михаил
Максимович Литвинов первым не только сформулировал понятие
«оригамики», но и показал, научил и создал в России новое движение
единомышленников, объединив их вокруг учебно-художественного Центра Оригами,
впоследствии преобразованного в Московский Клуб Оригами.

       Таким образом, можно сделать вывод о том, что оригами
появилось очень давно и в разное время, в разных странах использовалось для
различных целей: украшение стен храмов, передача посланий, обучение, игры. В
настоящее время оригами завоевало весь мир. С каждым годом, все большее
количество людей вовлекаются в это искусство.

Виды
оригами  (слайд 9)

Простое оригами— стиль оригами, придуманный британским
оригамистом Джоном Смитом. Этот стиль ограничен использованием только складок. Целью
оригами является облегчение занятий неопытным оригамистам, а также людям с
ограниченными двигательными навыками.

Складывание
по развёртке (слайд
10)

Развёртка (англ. creasepattern; паттерн складок) — один из видов
диаграмм оригами, представляющий собой чертёж, на котором изображены все
складки готовой модели. Складывание по развёртке сложнее складывания по
традиционной схеме, но по праву считается наиболее точной и практичной, ведь
представляет собою диаграмму, которая нанесена на лист и которой пользуется
мастер-оригамист перед складыванием. А линии, которые показаны на диаграмме,
есть не что иное, как будущие складки, из которых впоследствии сформируется
конечная фигура.

Мокрое складывание (слайд 11)
—
техника складывания, разработанная Акирой Йошизавой. Он использовал смоченную
водой бумагу для придания фигуркам плавности линий, выразительности, а также
жесткости. Особенно актуален данный метод для таких негеометрических
объектов, как фигурки животных и цветов — в этом случае они выглядят намного
естественней и ближе к оригиналу.

Модульное оригами (слайд 12)

Эта увлекательная техника — создание объёмных фигур из модулей.

Целая
фигура собирается из множества одинаковых модулей. Каждый модуль складывается
по правилам классического оригами из одного листа бумаги, а затем модули
соединяются путем вкладывания их друг в друга. Появляющаяся при этом сила
трения не даёт конструкции распасться.

Чтобы
сделать одну из таких работ, мы должны выполнить точный математический  расчет.

Надо
знать, сколько нужно листов бумаги, и сколько времени мы потратим на всю работу.

Для
выполнения таких работ потребуется треугольный модуль.

Схема изготовления
треугольного модуля:

Всего для изготовления рыбки потребуется 159 модулей: 2 красных,32
голубых, 9 оранжевых, 46 зеленых, 70 желтых.

(слайд
13) несколько моделей.

Одним
из наиболее часто встречающихся объектов модульного оригами является кусудама,
объёмное тело шарообразной формы (слайд 14).

Таким образом, можно сделать вывод о том, что существует несколько
видов оригами, каждый из которых интересен по-своему.

 Сегодня я покажу красоту
модульного оригами, связанную с многогранниками.

    Прежде чем перейти к технологии изготовления многогранников с
помощью оригами, познакомимся с «азбукой» и базовыми формами оригами (слайд
15).

    Условные знаки играют роль
своеобразных «нот», следуя которым можно воспроизвести любую работу.
Все обозначения в оригами можно разделить на линии, стрелки и
знаки.

    Освоив базовые формы, можно квадратный
лист, складывать разными способами.

Их немного
— одиннадцать, и у каждой своё имя.

1)             
Простые
базовые формы: треугольник, книга, дверь, воздушный змей;  (слайд 16)

2)             
Средние
базовые формы: блин, рыба, двойной треугольник, двойной квадрат;  (слайд 17)

3)             
Сложные
базовые формы: птица, катамаран, лягушка (слайд 18)

Отрабатывая технику
складывания различных элементов изделий оригами, следует обратить особое
внимание на правильное выполнение сгибов. Они должны быть практически
«острыми» и слои бумаги в них должны плотно прилегать друг к другу. В
противном случае при наложении сгибов друг на друга в последующих операциях
происходит смещение элементов и невозможно создать красивое, аккуратное
изделие. Поэтому после выполнения каждого отдельного этапа работы нужно проверять
«остроту» всех сгибов.

Применение математики в
оригами (слайды 19-24)

Оригами способствует активности как
левого, так и правого полушария мозга, так как требует одновременного контроля
за движениями обеих рук.

Проанализировав базовые формы оригами заметим,
что уже при первом знакомстве с этим искусством мы наблюдаем связь с
математикой  (слайд19-23)

( слайд 24)

Большинство классических моделей в
оригами выполняются из квадрата. В процессе изготовления простых моделей мы
знакомимся с очень нужными понятиями.

          В сложенном же виде оригами
представляет собой многогранник, фигуру с множеством плоских поверхностей. В
процессе складывания фигур оригами мы учимся легко ориентироваться в
пространстве и на листе бумаги, делить целое на части, находить вертикаль,
диагональ, узнаем многое другое, что относится к математике и геометрии.

Существует пять правильных многогранников, которые
называют Платоновыми телами (слайд 25). Они
составлены из правильных многоугольников (тетраэдр – 4 треугольника, октаэдр –
8 треугольников, икосаэдр – 20 треугольников, куб (гексаэдр) – 6 квадратов,
додекаэдр – 12 пятиугольников).

Эти удивительно симметричные правильные многогранники
получаются во время работы с бумагой. Правильные многогранники можно 
складывать по развертке, это один из видов оригами (слайд 26).  А мне
хотелось бы  остановиться на создании многогранников с помощью модуля.

Технология изготовления
многогранников с помощью оригами.

Складывание многогранников –
увлекательнейшее занятие, но вместе с тем и не простое. Оно требует
аккуратности, точности и высокого сосредоточения внимания. Вы можете
изготовить многогранник любого размера без всякой выкройки. Нужно только
выбрать размер листа бумаги. Кроме того оригамный многогранник всегда можно
разобрать, а его модули при этом не займут много места.

 Чаще всего для
оригами используют квадратные листы бумаги, но допускается и применение других
форматов. Например, прямоугольные листы (формата А₄ или половинки
квадратов), треугольники, пятиугольники, шести- и восьмиугольники.

Я сегодня познакомлю вас с моделями
многогранников, которые можно собрать с помощью одинаковых модулей. Сборка
модулей напоминает лего конструктор. Недаром модульное оригами называют  бумажным
ЛЕГО.

Первой моделью у нас будет куб.
Существует несколько способов сборки куба. Рассмотрим четыре способа, модели
которых у нас собраны  (слайд 27).

Способ
№1: Куб состоит из 6 граней
разного цвета.

Понадобится
6 квадратов 8х8 разного цвета. Из каждого квадрата формируем модуль. Модуль
состоит из одной детали формы прямоугольника. Схема сборки модуля.    Для
сборки необходимо 6 модулей разного цвета.

Способ
№2: Куб состоит из 6 граней.
Каждая грань состоит из двух цветов  (слайд 27).  

Понадобится 6 квадратов 14х14: 2 желтых, 2
оранжевых, 2 зелёных. Из каждого квадрата формируем модуль. Модуль состоит
из одной детали формы параллелограмма. Схема сборки модуля. Для сборки необходимо 6
модулей: 2 желтых, 2 оранжевых, 2 зелёных.

Способ №3: Куб
состоит из 6 граней. Каждая грань состоит из двух цветов (слайд 27).  

Понадобится
12 прямоугольников 10х5: 6 светло-зеленых, 6 голубых. Модуль
состоит из двух деталей светло-зеленого и голубого цвета. Схемы сборки модуля.  Для сборки
необходимо 6 сдвоенных модулей. Результат похож на предыдущий способ, только
более плотный получается.

Способ №4: (слайд
27).

Куб
состоит из 6 граней. Каждая грань состоит из двух цветов.

Понадобится
6 квадратов 8х8: 2 желтых, 2 зеленых, 2 розовых. Из каждого квадрата формируем
модуль Сонобэ. Модуль состоит из одной детали формы параллелограмма. Схема
сборки модуля Сонобэ.  Для сборки необходимо 6 модулей.

Вторая модель тетраэдр. Понадобится 1 квадрат 15х15. Делаются сгибы по схеме (слайд
28).

Третья модель октаэдр. Делаются сгибы по схеме (слайд 28).

Четвертая  модель додекаэдр    (слайд 28).

Понадобится
3 листа А₄. Делим его на 4 равные части. Получим 12 прямоугольников (10,5смх14,8см).
Мы взяла 6 разных цветов, поэтому у нас получилось по 2 прямоугольника разного
цвета         ( красный, синий, зелёный, светло-зеленый, жёлтый, розовый).

Пятая модель звездчатый октаэдр    (слайд 28).

Понадобится 12 квадратов
8х8:                     4 желтых, 4 зеленых, 4розовых. Для
сборки потребуется 12 модулей Сонобэ.

Мир
многогранников велик. Можно еще много осваивать моделей и их сборку из модулей.
Я думаю, что это очень увлекательное занятие. Будем  продолжать собирать
коллекцию многогранников из оригами. Например, вот такой.

А так же есть ещё одно очень интересное направление с помощью
оригами  это математические головоломки. Например,

Задание: Из
данных деталей собрать куб (слайд
29).

Освоив технику сборки кубика, мы сделали кубики меньших размеров.
Склеили детали между собой по схеме. Получили такую головоломку.

Сделав несколько таких головоломок, можно будет применять их как
на уроках, так и на внеклассных мероприятиях. И в завершении своей работы я
хотела бы подарить буклет, в котором вы найдете информацию, как собрать кубик.

Заключение  (слайд 30).

   «Мышление начинается с удивления, от
удивления к знаниям – один шаг. А математика – замечательный предмет для
удивления»

(слайд 31) в процессе работы,
фото

Мастер- класс (слайд 32-39)

Способ
№2:      Возьмем 6 квадратов
10х10.

Схема сборки модуля способа №2