С помощью какой инструкции находится целая часть от деления приведите пример

Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.

Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.

Оператор деления

Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.

Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.

Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.

Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.

Примеры:

print(int(1) / int(2))
print(5 / 5)
print(1 / 3)

0.5
1.0
0.3333333333333333

Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.

Дополнительно хотелось бы отметить, что если точности типа данных float не достаточно, можно воспользоваться библиотекой decimal. В частности мы её использовали при написании программы «калькулятор» в отдельной статье.

Деление без остатка

Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».

В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».

Примеры нахождения целой части от деления:

print(5 // 2)
print(0 // 2)
print(1234 // 5.0)

2
0
246.0

В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.

Остаток

Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.

Примеры:

print(10 % 3)
print(5 % 10)
print(5 % 0.25)

1
5
0.0

Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.

Вот пример вывода чётных чисел из списка в консоль:

example_list = [3, 7, 2, 8, 1, 12]
for value in example_list:
    if value % 2 == 0:
        print(value)

2
8
12

Проблемы чисел с плавающей точкой

Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.

Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.

a = 0.1
for i in range(13):
    a += 0.1
print(a)

1.4000000000000001

Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.

Деление комплексных чисел

Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.

Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.

Пример:

print((5 + 8j) / 2)

(2.5+4j)

Сокращенные операции деления

Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную. То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:

	Полная форма	Краткая форма
Деление	a = a / b	a /= b
Целая часть	a = a // b	a //=b
Остаток	a = a % b	a %= b

Приведём пример:

a = 245
a %= 17
print(a)

7

Деление на ноль

Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.

Исключение следует обрабатывать, это можно сделать так:

try:
    print(24 / 0)
except Exception as e:
    print(e)

division by zero

Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e:.
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:

a = 14
b = None
if a == 0:
    print('делитель равен нулю!')
else:
    b = 345/a
    print('Операция выполнена, результат = ' + str(b))

Операция выполнена, результат = 24.642857142857142

Источник

Целая часть от деления — это результат деления одного числа на другое, который представляет собой наибольшее целое число, меньшее чем результат деления. Например, целая часть от деления 7 на 3 равна 2, поскольку наибольшее целое число, которое меньше, чем 7/3 (что равно 2,333…), это 2.

Целая часть от деления может быть полезна в решении различных задач, например, при округлении чисел. Она также может использоваться для определения остатка от деления — остаток от деления равен разности исходного числа и произведения целой части на делитель. Например, остаток от деления 7 на 3 равен 1 (7 — 3*2 = 1).

Чтобы вычислить целую часть от деления вручную, необходимо разделить одно число на другое и округлить результат вниз до ближайшего целого числа. Можно также использовать функции программирования, которые автоматически вычисляют целую часть от деления.

Содержание

Целая часть от деления: определение и примеры вычислений
Целая часть от деления: определение
Зачем нужна целая часть от деления?
Определение
Как вычислить целую часть от деления?
Примеры вычислений
Пример 1: деление целых чисел
Пример 2: деление десятичных дробей
Пример 3: деление отрицательных чисел

Целая часть от деления: определение и примеры вычислений

Целая часть от деления является одним из базовых математических понятий, которое необходимо знать для работы с числами. Ее обозначают с помощью символа «//». Целая часть от деления определяется как наибольшее целое число, которое меньше или равно результату деления двух чисел.

Пример: целая часть от деления числа 20 на 6 равна 3, так как 20/6=3.3333. Делая этот расчет вручную, мы получим, что 3*6=18, а 20-18=2. Поскольку 2<6, то ответом будет 3.

Еще один пример: целая часть от деления числа 14 на 3 равна 4, так как 14/3=4.6666. В данном случае, 4*3=12, а 14-12=2. Поскольку 2<3, то ответом является 4.

Возможно, вы столкнулись с целой частью от деления в некоторых подзадачах по программированию, когда вам нужно найти остаток от деления двух чисел. В таких сценариях вам может помочь математическая формула, которая позволяет найти остаток: остаток от деления двух чисел равен их сумме, умноженной на целую часть от деления первого числа на второе, минус первое число.

Два числа	Целая часть от деления	Остаток
20 и 6	3	2
14 и 3	4	2
17 и 5	3	2

Используя эту формулу, вы можете быстро найти остаток от деления двух чисел. Например, для чисел 20 и 6 целая часть от деления равна 3, а следовательно, остаток от деления будет равен 20-3*6=2.

Надеюсь, этот материал помог вам лучше понять, что такое целая часть от деления и как ее можно вычислить. Знание этого понятия может быть полезным, как при выполнении математических задач на бумаге, так и в технических областях, где требуется работать с числами и делениями.

Целая часть от деления: определение

Целая часть от деления — это часть результата деления двух чисел, которая находится перед запятой и не содержит дробной части. Например, целая часть от деления числа 10 на число 3 равна 3.

Если результат деления является целым числом, целая часть равна этому числу. Например, целая часть от деления числа 12 на число 6 равна 2.

Определять целую часть от деления можно как с помощью целочисленного деления, так и методом вычитаний. Если нет возможности использовать целочисленное деление, можно использовать метод вычитаний, который заключается в том, чтобы вычитать делитель из делимого до тех пор, пока результат не станет меньше делителя. Число вычитаний будет равно целой части результата.

Целая часть от деления имеет множество применений в математике и программировании, так как позволяет определить количество целых объектов, которые могут быть размещены в другом объекте определенного размера.

Зачем нужна целая часть от деления?

Целая часть от деления — это результат деления двух чисел, округленный в меньшую сторону до ближайшего целого числа. Этот результат имеет широкое применение в математике и программировании, особенно при работе с длинными числами.

Целая часть от деления часто используется, например, при делении одного числа на другое, чтобы определить, сколько раз одно число содержится в другом без остатка. Помимо этого, целая часть от деления может использоваться для обработки числовых данных, например, при нахождении среднего значения или максимального значения в массиве чисел.

В программировании целая часть от деления может быть использована для определения четности или нечетности числа, а также для проверки делимости чисел нацело. Также этот результат может быть полезен при вычислении сложности алгоритмов и оптимизации кода.

В общем, целая часть от деления — это очень полезный математический инструмент, который используется в различных сферах деятельности, от науки и техники до финансов и экономики.

Определение

Целая часть от деления — это число, которое получается при делении одного целого числа на другое. Ответом на такое деление является частное, которое может быть дробным числом.

Целая часть от деления — это наибольшее целое число, которое меньше или равно частному от деления.

Например, если мы делим число 15 на 3, мы получим частное 5. Целая часть от деления будет равна 5, так как от 5 до 6 не будет никаких целых чисел.

Обычно целая часть от деления выглядит как целое число, но может быть выражена и в виде дроби с нулевым числителем.

Как вычислить целую часть от деления?

Целая часть от деления — это результат деления, округленный до целого числа. Например, при делении 15 на 4, результат будет 3.75, а целая часть — 3.

Вычисление целой части от деления может быть произведено с помощью оператора «целочисленное деление» (//) в большинстве языков программирования. Например, 15 // 4 вернет целую часть от деления равную 3.

Также можно использовать функцию floor() в некоторых языках программирования, которая округлит результат деления вниз до ближайшего целого числа. Например, floor(15 / 4) также вернет целую часть от деления равную 3.

Необходимость вычисления целой части от деления может возникнуть в случае разделения числа на равные группы, например, при распределении товаров по корзинам на складе или при подсчете оставшихся дней до события.

Примеры вычислений

Рассмотрим примеры вычислений целой части от деления. Допустим, нам нужно найти целую часть от деления числа 25 на 4. Для этого необходимо разделить 25 на 4:

25 ÷ 4 = 6,25

Целая часть от полученного результата будет являться ответом задачи:

Целая часть от 6,25 равна 6

Еще один пример: найдем целую часть от деления числа 60 на 7. Проведем соответствующие вычисления:

60 ÷ 7 = 8,57

Целая часть от 8,57 равна 8

Можно заметить, что если число кратно делителю, то результат будет являться целым числом. Например, если нужно найти целую часть от деления числа 12 на 3, ответ будет равен 4, так как 12 кратно 3.

Пример 1: деление целых чисел

Деление целых чисел происходит с использованием оператора деления «/». Например, вычислим результат деления 15 на 3:

Сначала необходимо разделить целое число 15 на целое число 3.
Результатом деления будет десятичная дробь, но так как мы используем целые числа, будет получена только целая часть.
15 / 3 = 5

Итак, результат деления 15 на 3 равен 5. Ваша ответственность — проверить результат. Убедитесь, что при умножении 5 на 3 получается исходное число:

5 * 3 = 15

Теперь вы знаете, как вычислить целую часть от деления двух целых чисел. Попробуйте сами вычислить целую часть от деления других чисел.

Пример 2: деление десятичных дробей

Деление десятичных дробей может быть немного сложнее, но техника такая же, как и при делении целых чисел.

Например, рассмотрим задачу деления 0,25 на 0,5.

Сначала нужно привести числа к общему знаменателю, то есть домножить каждую дробь на 100.
Теперь получим 25/100 и 50/100.
Сокращаем дроби до простого вида: 25/100 = 1/4, а 50/100 = 1/2.
Делим 1/4 на 1/2: 1/4 ÷ 1/2 = 1/4 × 2/1 = 2/4.
Упрощаем дробь 2/4: 2/4 = 1/2.

Таким образом, результатом деления 0,25 на 0,5 является 0,5.

Не забывайте проверять результат, умножив делитель на частное, чтобы убедиться, что получится исходное делимое.

Пример 3: деление отрицательных чисел

Деление отрицательных чисел также можно производить по правилам обычного деления. Однако, при вычислении целой части от деления отрицательных чисел, необходимо учитывать особенности знаков.

Например, если нужно вычислить целую часть от деления -9 на -4, то сначала выполняем обычное деление:

Ответ: -9 / -4 = 2 (остаток -1). При этом, целая часть от деления отрицательных чисел — это число, которое получается при делении без учета знаков, а затем умножается на исходные знаки.

То есть в данном случае, -2 (результат деления без учета знаков) умножаем на исходные знаки (- * — = +) и получаем 2 как целую часть от деления -9 на -4.

Источник

Оператор деления

Деление без остатка

Примеры нахождения целой части от деления:

Остаток

Вот пример вывода чётных чисел из списка в консоль:

Проблемы чисел с плавающей точкой

Деление комплексных чисел

Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.

Сокращенные операции деления

Полная форма	Краткая форма
Деление	a = a / b	a /= b
Целая часть	a = a // b	a //=b
Остаток	a = a % b	a %= b

Деление на ноль

Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.

Исключение следует обрабатывать, это можно сделать так:

Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e: .
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:

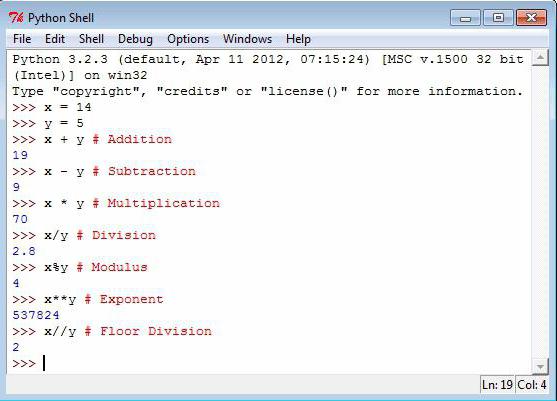
Python – простой, современный язык для написания кода. Он обладает мощными библиотеками, способными вычислить любое выражение. Python выступает основным конкурентом для Matlab и Octave. Запустив в интерактивном режиме Python, остаток от деления пользователь сможет найти без труда. Но это еще не все! «Питон» может выступить мощным калькулятором.

Понятие оператора

Чтобы без труда найти в Python остаток от деления, нужно разобраться с некоторыми определениями. Оператор – знак или строка, позволяющие произвести математическое, побитовое, логическое и другое вычисление. Выражения или числа, вводимые пользователем, чтобы найти в Python 3 остаток от деления, тождественность сочетания или сравнения, называются операндами.

Разделяют следующие виды операторов:

арифметические;
побитовые;
логические;
операторы присваивания;
сравнения;
членства;
тождественности.

Проще говоря, в примере «15 — 5» оператором является знак «–», операндами – 15 и 5. Это арифметическая операция с целыми числами. Если взять к рассмотрению выражение «True and True», то оператором здесь выступает «and», а операндами – «True» и «True». Этот пример можно отнести к логическому типу.

Целые и вещественные числа. Математические операции и вывод результата

Если рассматривать математические операции над целыми и дробными числами, то операторами выступают +, -, *, /, **, //, %. С первыми тремя всё понятно. Они обозначают, соответственно, сложение, вычитание, умножение. Оператор «**» указывает на необходимость возведения в степень.

Знаки одинарного (/) и двойного (//) деления отличаются. Если первый выдает в решении вещественное число, то второй необходим для нахождения целой части от деления. К примеру, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но есть закономерность. Знак «/» выведет целое число как результат, если и делитель, и делимое – также целые. Чтобы найти в Python остаток от деления, нужно воспользоваться оператором «%». По аналогии с тем же «Турбо Паскалем» «%» сопоставим с функцией mod. К примеру, 9%2 = 1, т.е. в Python остаток от деления в данном случае равняется 1. Рассмотрим еще примеры.

Чтобы произвести деление без остатка, Python предлагает воспользоваться функцией divmod(х,у). В данном случае х – делимое, у – делитель. Для выражения divmod (9,3) программа выдаст следующий результат (3,0). Это означает, что целая часть от деления равняется 3, а остаток – 0.

Математические операции можно выполнять без присваивания значения переменной. Тогда результат выдается автоматически. Если же код содержит присваивание переменной, то вывести результат на экран можно посредством оператора print.

Модуль math

Для удобства пользователей разработчики предлагают мощный модуль math, способный работать с любыми типами чисел и выполнять дополнительные функции.

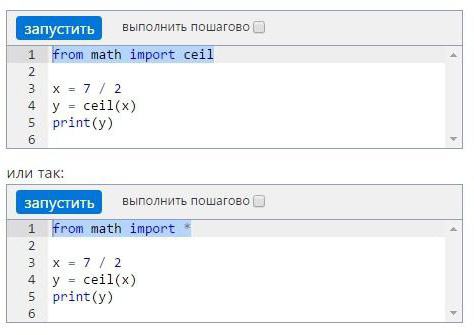
Чтобы подключить библиотеку, нужно прописать в начале программного кода следующую строку: import math. Такая команда позволит подгрузить в программный код все функции, имеющиеся в модуле math. Тогда для подключения определенного блока из библиотеки нужно постоянно прописывать его. К примеру, x = math.ceil(5.6).

Если в программе будет часто использоваться один и тот же блок, то можно импортировать только его. К примеру, нужно произвести ряд округлений до ближайшего целого числа в большую сторону. Тогда код прописывается следующим образом: from math import ceil или from math import *. В обоих случаях дальнейший код по округлению результата не изменится.

Стандартные функции арифметики в Python

Чтобы вычислить в Python остаток от целочисленного деления, не всегда нужно подгружать библиотеку math. Некоторые функции являются встроенными.

Превращает вещественное число в целое, т.е. дробная часть «отсекается».

Происходит округление выражения до ближайшего целого.

Используется для округления дробной части до n знаков после запятой

Находит модуль выражения

Функции, для которых необходимо подключение библиотеки (нужно изначально вписать from math import *), можно увидеть в следующей таблице.

Функция необходима для округления числа до большего целого («вверх»)

Функция требуется, чтобы округлить число до меньшего целого («вниз»)

Вычисляет корень из числа

Необходима для нахождения логарифма. Если указать основание, то и вычисление будет соответствующим.

Выводит основание натурального логарифма

Вычисление тригонометрических функций, где х выражен в радианах

Находит полярный угол точки, координаты которой задаются х и у

Необходима для преобразования угла из радиан в градусы

Функция, необходимая для преобразования угла, заданного в градусах, в радианы

Выводит значение константы π

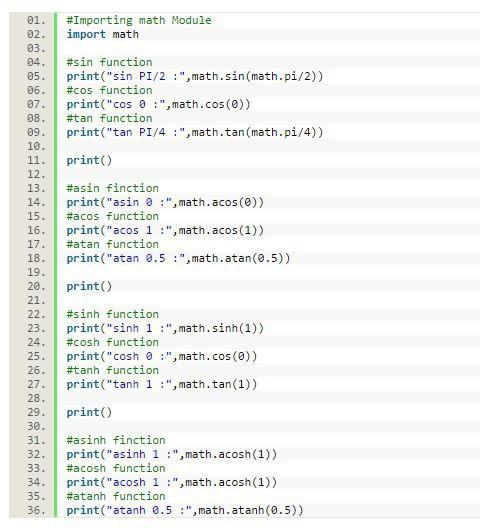
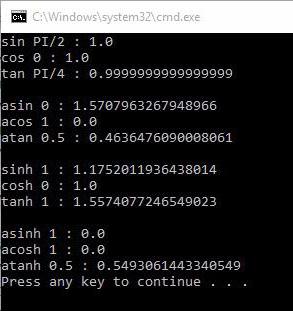
В качестве примера ниже приведен код с использованием математических операторов.

Результат выведен следующим образом.

В модуле math гораздо больше функций. Здесь указаны наиболее встречающиеся.

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y[, z])	x y по модулю (если модуль задан)

Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).

Битовые операции

Над целыми числами также можно производить битовые операции

Дополнительные методы

int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

Системы счисления

Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:

int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.
oct(х) — преобразование целого числа в восьмеричную строку.

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

Простенькие примеры работы с числами:

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.

Модуль math предоставляет более сложные математические функции.

Модуль random реализует генератор случайных чисел и функции случайного выбора.

Комплексные числа (complex)

В Python встроены также и комплексные числа:

Также для работы с комплексными числами используется также модуль cmath.

Оператор деления

Деление без остатка

Примеры нахождения целой части от деления:

Остаток

Вот пример вывода чётных чисел из списка в консоль:

Проблемы чисел с плавающей точкой

Деление комплексных чисел

Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.

Сокращенные операции деления

x \| y	Побитовое или
x ^ y	Побитовое исключающее или
x & y	Побитовое и
x > y	Битовый сдвиг вправо
Инверсия битов

Полная форма	Краткая форма
Деление	a = a / b	a /= b
Целая часть	a = a // b	a //=b
Остаток	a = a % b	a %= b

Деление на ноль

Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.

Исключение следует обрабатывать, это можно сделать так:

Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e: .
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:

Операторы Python

В этом руководстве речь пойдет об операторах языка программирования Python. Вы узнаете об арифметических, логических и битовых операторах, а также операторах сравнения, присваивания, принадлежности, тождественности и их синтаксисе. Все это будет проиллюстрировано примерами.

Оператор в Python — это символ, который выполняет операцию над одним или несколькими операндами.
Операндом выступает переменная или значение, над которыми проводится операция.

Введение в операторы Python

Операторы Python бывают 7 типов:

Арифметические операторы
Операторы сравнения
Операторы присваивания
Логические операторы
Операторы принадлежности
Операторы тождественности
Битовые операторы

Арифметические операторы Python

Этот тип включает операторы для проведения базовых арифметических операций.

Сложение (+)

Складывает значение по обе стороны оператора.
Пример:

Вычитание (-)

Вычитает значение правой стороны из значения в левой.
Пример:

Умножение (*)

Перемножает значения с обеих сторон оператора.
Пример:

Деление (/)

Делит значение левой стороны на значение правой. Тип данных результата деления — число с плавающей точкой.
Пример:

Возведение в степень (**)

Возводит первое число в степень второго.
Пример:

Деление без остатка (//)

Выполняет деление и возвращает целочисленное значение частного, убирая цифры после десятичной точки.
Пример:

Деление по модулю (остаток от деления) (%)

Выполняет деление и возвращает значение остатка.
Пример:

Операторы сравнения

Операторы сравнения в Python проводят сравнение операндов. Они сообщают, является ли один из них больше второго, меньше, равным или и то и то.

Меньше (

Этот оператор проверяет, является ли значение слева меньше, чем правое.
Пример:

Больше (>)

Проверяет, является ли значение слева больше правого.

Пример:

Меньше или равно (

Проверяет, является ли левая часть меньше или равной правой.
Пример:

Больше или равно (>=)

Проверяет, является ли левая часть больше или равной правой.
Пример:

Равно (==)

Этот оператор проверяет, равно ли значение слева правому. 1 равна булевому True , а 2 (двойка) — нет. 0 равен False .
Пример:

Не равно (!=)

Проверяет, не равно ли значение слева правому. Оператор <> выполняет ту же задачу, но его убрали в Python 3.

Когда условие выполнено, возвращается True . В противном случае — False . Это возвращаемое значение можно использовать в последующих инструкциях и выражениях.
Пример:

Операторы присваивания

Оператор присваивания присваивает значение переменной. Он может манипулировать значением до присваивания. Есть 8 операторов присваивания: 1 простой и 7 с использованием арифметических операторов.

Присваивание (=)

Присваивает значение справа левой части. Стоит обратить внимание, что == используется для сравнения, а = — для присваивания.
Пример:

Сложение и присваивание (+=)

Суммирует значение обеих сторон и присваивает его выражению слева. a += 10 — это то же самое, что и a = a + 10 .

То же касается и все остальных операторов присваивания.
Пример:

Вычитание и присваивание (-=)

Вычитает значение справа из левого и присваивает его выражению слева.
Пример:

Деление и присваивание (/=)

Делит значение слева на правое. Затем присваивает его выражению слева.
Пример:

Умножение и присваивание (*=)

Перемножает значения обеих сторон. Затем присваивает правое левому.
Пример:

Деление по модулю и присваивание (%=)

Выполняет деление по модулю для обеих частей. Результат присваивает левой части.
Пример:

Возведение в степень и присваивание (**=)

Выполняет возведение левой части в степень значения правой части. Затем присваивает значение левой части.
Пример:

Деление с остатком и присваивание (//=)

Выполняет деление с остатком и присваивает результат левой части.
Пример:

Это один из важных операторов Python

Логические операторы Python

Это союзы, которые позволяют объединять по несколько условий. В Python есть всего три оператора: and (и), or (или) и not (не).

И (and)

Если условия с двух сторон оператора and истинны, тогда все выражение целиком считается истинным.
Пример:

Или (or)

Выражение ложно, если оба операнда с двух сторон ложные. Если хотя бы одно из них истинное, то и все выражение истинно.
Пример:

Не (not)

Этот оператор инвертирует булевые значения выражения. True превращается в False и наоборот. В примере внизу булево значение 0 — False . Поэтому оно превращается в True .
Пример:

Операторы принадлежности

Эти операторы проверяют, является ли значение частью последовательности. Последовательность может быть списком, строкой или кортежем. Есть всего два таких оператора: in и not in .

Проверяет, является ли значение членом последовательности. В этом примере видно, что строки fox нет в списке питомцев. Но cat — есть, поэтому она возвращает True . Также строка me является подстрокой disappointment . Поэтому она вернет True .
Пример:

Нет в (not in)

Этот оператор проверяет, НЕ является ли значение членом последовательности.
Пример:

Операторы тождественности

Эти операторы проверяют, являются ли операнды одинаковыми (занимают ли они одну и ту же позицию в памяти).

Это (is)

Если операнды тождественны, то вернется True . В противном случае — False . Здесь 2 не является 20 , поэтому вернется False . Но ‘2’ — это то же самое, что и «2» . Разные кавычки не меняют сами объекты, поэтому вернется True .
Пример:

Это не (is not)

2 — это число, а ‘2’ — строка. Поэтому вернется True .
Пример:

Битовые операторы Python

Эти операторы работают над операндами бит за битом.

Бинарное И (&)

Проводит побитовую операцию and над двумя значением. Здесь бинарная 2 — это 10 , а 3 — 11 . Результатом побитового and является 10 — бинарная 2 . Побитовое and над 011 (3) и 100 (4) выдает результат 000 (0).
Пример:

Бинарное ИЛИ (|)

Проводит побитовую операцию or на двух значениях. Здесь or для 10 (2) и 11 (3) возвращает 11 (3).
Пример:

Бинарное ИЛИ НЕТ (^)

Проводит побитовую операцию xor (исключающее или) на двух значениях. Здесь результатом ИЛИ НЕ для 10 (2) и 11 (3) будет 01 (1).
Пример:

Инвертирующий оператор (

Он возвращает инвертированные двоичные числа. Другими словами, переворачивает биты. Битовая 2 — это 00000010 . Ее инвертированная версия — 11111101 . Это бинарная -3 . Поэтому результат -3 . Похожим образом

1 равняется -2 .
Пример:

Еще раз, инвертированная -3 — это 2 .

Бинарный сдвиг влево (

Он сдвигает значение левого операнда на позицию, которая указана справа. Так, бинарная 2 — это 10 . 2 сдвинет значение на две позиции влево и выйдет 1000 — это бинарная 8 .
Пример:

Бинарный сдвиг вправо (>>)

Сдвигает значение левого оператора на позицию, указанную справа. Так, бинарная 3 — это 11 . 3 >> 2 сдвинет значение на два положение вправо. Результат — 00 , то есть 0 . 3 >> 1 сдвинет на одну позицию вправо, а результатом будет 01 — бинарная 1 .
Пример:

Выводы

В этом уроке были рассмотрены все 7 типов операторов Python. Для каждого был предложен пример в IDE. Для понимания особенностей работы операторов нужно продолжать с ними работать, использовать в условных конструкциях и объединять.

Числа: целые, вещественные, комплексные

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y[, z])	x y по модулю (если модуль задан)

Битовые операции

Над целыми числами также можно производить битовые операции

x \| y	Побитовое или
x ^ y	Побитовое исключающее или
x & y	Побитовое и
x > y	Битовый сдвиг вправо
Инверсия битов

Дополнительные методы

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

Системы счисления

int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.
oct(х) — преобразование целого числа в восьмеричную строку.

Вещественные числа (float)

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

Простенькие примеры работы с числами:

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

Модуль math предоставляет более сложные математические функции.

Модуль random реализует генератор случайных чисел и функции случайного выбора.

Комплексные числа (complex)

В Python встроены также и комплексные числа:

Также для работы с комплексными числами используется также модуль cmath.

Арифметические операции

На этом занятии рассмотрим виды и работу арифметических операторов в Python. И как уже говорили, в этом языке имеется три базовых типа для представления чисел:

int – для целочисленных значений;
float – для вещественных;
complex – для комплексных.

Оператор

Описание

Приоритет

сложение

вычитание

умножение

деление

остаток деления

возведение в степень

И введем несколько определений:

Операнд – то, к чему применяется оператор. Например, в умножении 5 * 2 есть два операнда: левый операнд равен 5, а правый операнд равен 2. Иногда их называют «аргументами» вместо «операндов».

Унарным называется оператор, который применяется к одному операнду.

Обратите внимание как записаны два оператора в одну строчку: они разделены точкой с запятой. Так тоже можно делать. Если каждый оператор начинается с новой строки, то точку с запятой ставить не обязательно, если пишем несколько операторов в одну строчку, то они разделяются точкой с запятой.

Бинарным называется оператор, который применяется к двум операндам.

Тот же минус существует и в бинарной форме:

Раз мы начали говорить об операциях + и -, то продолжим и отметим, что, в общем случае, можно использовать унарный плюс и минус, например:

Конечно, +a это то же самое, что и a, поэтому, в основном, используется унарный минус. По приоритету унарные операции выше бинарных операций. Например, вот такая запись:

означает, что число –a возводится в степень 2, то есть, унарный минус имеет больший приоритет, чем бинарная операция ** возведения в степень.

Если же используются бинарные сложение и вычитание:

то их приоритет становится наименьшим среди всех арифметических операций (они выполняются в последнюю очередь).

Следующая бинарная операция умножение работает так, как мы привыкли ее использовать в математике:

Здесь сначала выполнится умножение, а затем – сложение. Если необходимо изменить приоритет выполнения операций, то используются круглые скобки:

Далее, деление двух чисел (или переменных) можно выполнить двумя способами. Первый – традиционный, делает деление, привычное в математике, например:

получим ожидаемый результат 1,5. Однако те из вас, кто имеет опыт программирования на таких языках как С++ или Java, знают, что при делении двух целочисленных значений, результат также получался целочисленным. Но в Python это не так! Его арифметические операции работают в соответствии с классическими правилами математики и деление здесь – это всегда полноценное деление двух значений, какими бы они ни были.

Однако, если все же требуется выполнить целочисленное деление (то есть, с отбрасыванием дробной части), то используется такой оператор:

И, как видите, теперь результат 1, а не 1,5. Причем, это целочисленное деление будет выполняться и с вещественными числами:

Вот такие два оператора деления существуют в Python.

Если же хотим вычислить остаток от целочисленного деления, то используется оператор:

С положительными целыми числами он работает также как и во многих других языках программирования. Например,

и так далее, мы будем получать числа от 0 до 4. Но с отрицательными числами вычисления будут отличаться от того же языка С++. Например,

Почему так? Дело в том, что когда то давно инженеры фирмы Intell неверно математически реализовали данную операцию. И язык С++ как наследник этой интеловской архитектуры реализует данную операцию путем вынесения знака «-» за скобки и вычисления обычного остатка от деления. Язык же Python делает это так, как принято в математике. Сначала находится ближайшее наименьшее число кратное 5. Это число -10 (для числа -9) и остаток берется как разность между этими числами:

то есть, остатки всегда будут положительными в диапазоне от 0 до 4, как это и должно быть по математике.

Все рассмотренные операторы (*, /, //, %) имеют одинаковый приоритет и выполняются слева-направо. То есть, если записать

то это следует интерпретировать как формулу

Следующая операция – возведение в степень. В самом простом варианте она записывается так:

здесь x, y могут быть и дробными числами. Например:

Это будет соответствовать извлечению квадратного корня из 1,96. Если запишем такую конструкцию:

то получим кубический корень из 27. Причем, обратите внимание, круглые скобки у степени здесь обязательны, т.к. приоритет операции ** выше, чем у деления. Если записать вот так:

то это будет эквивалентно такому выражению:

Вот на это следует обращать внимание. И еще один нюанс. Операция возведения в степень выполняется справа-налево. То есть, если записать вот такую строчку:

Это будет эквивалентно степени:

Сначала (справа) вычисляется 3**2 = 9, а затем, 2**9 = 512. Все остальные арифметические операции работают слева-направо.

Используя оператор присваивания совместно с арифметическими операторами, можно выполнять некоторые полезные арифметические преобразования переменных. Например, очень часто требуется увеличить или уменьшить некую переменную на определенное число. Это можно сделать вот так:

Но, можно и короче, вот так:

Они довольно часто используются в программировании. Также, помимо сложения и вычитания, можно записывать и такие выражения:

То есть, здесь до оператора присваивания можно записывать любую арифметическую операцию.

Все рассмотренные арифметические операции можно выполнять и с комплексными числами:

Кроме операции целочисленного деления // и вычисления остатка от деления %. Дополнительно у объектов комплексных чисел есть свойства:

для взятия действительной и мнимой части. И полезный метод:

для получения комплексно-сопряженного числа.

В языке Python имеются встроенные функции для работы с числами. Наиболее полезные, следующие:

Название

Описание

вычисляет модуль числа x

round(x)

округляет x до ближайшего целого

min(x1, x2,…,x_n)

находит минимальное, среди указанных чисел

max(x1, x2,…,x_n)

находит максимальное, среди указанных чисел

pow(x, y)

возводит x в степень y

Также в языке Python имеется стандартная библиотека math, которая содержит большое количество стандартных математических функций. Чтобы ей воспользоваться, необходимо вначале программы подключить эту библиотеку. Делается это с помощью ключевого слова import, за которым указывается имя библиотеки:

После этого становятся доступными следующие полезные функции:

Название

Описание

math.ceil(x)

возвращает ближайшее наибольшее целое для x

math.floor(x)

возвращает ближайшее наименьшее целое для x

math.fabs(x)

возвращает модуль числа x

math.factorial(x)

вычисляет факториал x!

math.exp(x)

вычисляет e**x

math.log2(x)

вычисляет логарифм по основанию 2

math.log10(x)

вычисляет логарифм по основанию 10

math.log(x, [base])

вычисляет логарифм по указанному основанию base (по умолчанию base = e – натуральный логарифм)

math.pow(x, y)

возводит число x в степень y

math.sqrt(x)

вычисляет квадратный корень из x

Тригонометрические функции

math.cos(x)

вычисляет косинус x

math.sin(x)

вычисляет синус x

math.tan(x)

вычисляет тангенс x

math.acos(x)

вычисляет арккосинус x

math.asin(x)

вычисляет арксинус x

math.atan(x)

вычисляет арктангенс x

Математические константы

math.pi

число пи

math.e

число e

Помимо этих есть и другие математические функции. При необходимости, о них можно почитать в официальной документации языка Python.

Применение этих функций вполне очевидно, например, их можно вызвать вот так:

И так далее. Вот так работают арифметические операции в Python и вот такие математические функции имеются в стандартной библиотеке math.

Видео по теме

Python 3 #1: установка и запуск интерпретатора языка

Python 3 #2: переменные, оператор присваивания, типы данных

Python 3 #3: функции input и print ввода/вывода

Python 3 #4: арифметические операторы: сложение, вычитание, умножение, деление, степень

Python 3 #5: условный оператор if, составные условия с and, or, not

Python 3 #6: операторы циклов while и for, операторы break и continue

Python 3 #7: строки — сравнения, срезы строк, базовые функции str, len, ord, in

Python 3 #8: методы строк — upper, split, join, find, strip, isalpha, isdigit и другие

Python 3 #9: списки list и функции len, min, max, sum, sorted

Python 3 #10: списки — срезы и методы: append, insert, pop, sort, index, count, reverse, clear

Python 3 #11: списки — инструмент list comprehensions, сортировка методом выбора

Python 3 #12: словарь, методы словарей: len, clear, get, setdefault, pop

Python 3 #13: кортежи (tuple) и операции с ними: len, del, count, index

Python 3 #14: функции (def) — объявление и вызов

Python 3 #15: делаем «Сапер», проектирование программ «сверху-вниз»

Python 3 #16: рекурсивные и лямбда-функции, функции с произвольным числом аргументов

Python 3 #17: алгоритм Евклида, принцип тестирования программ

Python 3 #18: области видимости переменных — global, nonlocal

Python 3 #19: множества (set) и операции над ними: вычитание, пересечение, объединение, сравнение

Python 3 #20: итераторы, выражения-генераторы, функции-генераторы, оператор yield

Python 3 #21: функции map, filter, zip

Python 3 #22: сортировка sort() и sorted(), сортировка по ключам

Python 3 #23: обработка исключений: try, except, finally, else

Python 3 #24: файлы — чтение и запись: open, read, write, seek, readline, dump, load, pickle

Python 3 #25: форматирование строк: метод format и F-строки

Python 3 #26: создание и импорт модулей — import, from, as, dir, reload

Python 3 #27: пакеты (package) — создание, импорт, установка (менеджер pip)

Python 3 #28: декораторы функций и замыкания

Python 3 #29: установка и порядок работы в PyCharm

© 2020 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Источник

Итак, мы разделили число на тысячи и вывели, сколько тысяч оно содержит. Теперь проделаем то же самое для сотен, десятков и единиц, изменив лишь несколько значений и вывод.

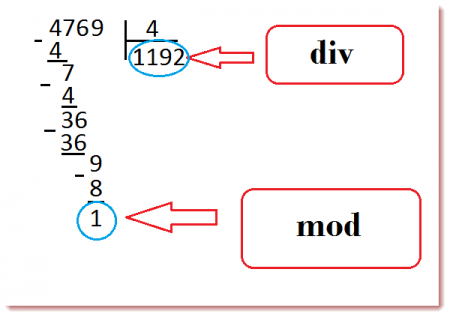
Что такое div и mod в паскале

Это вопрос: Что такое операции mod и div в Паскале? Как вы можете работать с нами?

Уровень сложности : легко.

Я постараюсь быть кратким и сразу скажу, что эти операции работают только с целыми числами, то есть с целыми числами и т.д. Во-первых, операция div: эта операция используется для нахождения целочисленной части деления. Как его следует понимать? Предположим, у нас есть код:

Зададим n равным 1. Почему? Как я уже сказал, div ищет целую часть деления, например, у нас 12 делится на 10, это дает 1.2. Целая часть деления равна 1. И вот что делает операция div, если мы скажем 12 div 2, ответ будет 6.0, целая часть равна 6. Это как деление 12 на 10, но в ответ записывается только целая часть деления.

Затем операция mod: эта операция уже ищет остаток от деления. Не думайте, что это дробь, не путайте!

Предположим, что существует код:

Рассмотрим небольшой пример: Предположим, существует число 123:

Обычно вы начинаете с последней цифры, в данном случае это 3. Чтобы вывести ее, мы должны сделать следующее:

То есть, мы делим 123 на 10, результат — 12,3, а остаток — 3. Первая цифра есть. Следующая цифра — 2. Сначала мы вычтем последнюю цифру, которая равна 3, с помощью div, а затем с помощью mod найдем вторую цифру:

То есть, сначала мы имеем 12 из-за div, а затем, используя mod, мы имеем 2. Последняя цифра может быть найдена следующим образом:

Например, вот так. Возможно, вы не сразу поймете это, но для этого нужно немного практики. Удачи! Спасибо за внимание!

Привет всем, как дела? Что случилось? Хорошо, я понял. Давайте не будем много говорить и будем дружелюбны, проходите, располагайтесь, чувствуйте себя комфортно. Снаружи солнце порабощает планету каждый день, я люблю это и с нетерпением жду еще одной теплой, грязной весны с большим количеством воды. Но есть золотая середина: тепло, птицы, растительность, легкая куртка. А как вы относитесь к весне? В этой части мы поговорим еще о двух функциях DIV и MOD, в предыдущей части мы говорили о математических операциях, сегодняшние функции также по сути являются таковыми. Вот так =)

DIV, MOD или обычное деление

DIV и MOD похожи на простое деление, но они все же для чего-то существуют, поэтому должна быть разница. Вспомните начальную школу и математику, когда вы учили только умножение и деление, когда вы еще не знали, что станете программистом и будете работать по принципу «ты — программист» или передатчиком. Шутки в сторону, давайте подумаем о делении столбцов. Возьмите 23 и разделите в столбик, как мы делали это в школе, на число 10.

Поэтому мы разделили 23 на 10. У нас осталось целое число 2 и остаток 3. Проще говоря, наш ответ — два целых числа и три десятых (2,3). Хорошо, это было обычное деление, но как бы это выглядело в случае MOD и DIV?

MOD — если разделить число с помощью функции MOD, то в качестве ответа мы получим остаток. В приведенном выше примере, если мы разделим число на Mod, а не на обычное деление, ответ будет 3.

DIV — наоборот, если мы делим с помощью DIV, то ответом будет только целая часть — 2.

Pascal

Откройте PascalABC и напишите программу

Объявите две переменные с целым типом данных

Затем присвойте значение переменной «a» и установите переменную «b» равной переменной «a».

Отлично, теперь выведите ответ для обычного деления на 100

Теперь выполним то же деление, но с DIV и MOD вместо обычного деления. Разделите переменную «a» на DIV, а переменную «b» на MOD и посмотрите, что получится.

Как видите, div обозначает целую часть, а mod — остаток.

Деление нацело ( div )

Целочисленное деление — это деление, при котором целое число делится на другое целое число. Результатом является целая часть его коэффициента.

Результатом операции является целое число, полученное в результате деления, или, точнее, целая часть результата деления.

15div3=5//результат обычного деления 514div3=4//результат обычного деления 4.6666663div2=1//результат обычного деления 1.5

Остаток от деления ( mod )

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю. 16: 7 = 2 (остаток 2) 23: 8 = 2 (остаток 7)

Результатом является целое число, которое представляет собой разность между делимым числом и следующим меньшим или равным ему целым числом, деленным на делитель.

15мод3=0//результат 15-1514мод3=2//результат 14-123мод2=1//score 3-2

Примечание: Операции div и mod применяются только к целым числам.

Используйте mod для определения кратности, т.е. делится ли число на четное число. Например, что числа 2, 6, 12, 24 делятся на два (четные числа). Оказывается, что все числа, которые не делятся на два, являются нечетными. Или числа 5, 10, 15, 20 кратны 5.

Рассмотрите несколько примеров использования этих операций в программировании.

Задание 1: Укажите размер файла в байтах и найдите количество полных килобайт, которые он занимает (1 килобайт = 1024 байта), используя операцию деления на целое число.

Решение:

Программаzadanie1;varb:Целое число;начатьчитать(b);b:=bdiv1024;пишите.(b);Конец.

Задача 2. Дано трехзначное число k. Найдите сумму цифр числа S.

Решение:

ПрограммаЗадание2;vark,s,c1,c2,c3:Целое число;начатьчитать(k);с1:=kмод10;с2:=(kdiv10)мод10;с3:=kмод100;s:=c1+c2+c3;пишите.(s);Конец.

Стандартные функции PascalABC

При написании программ на языке Pascal для выполнения вычислений можно использовать функции, доступные в среде программирования. Ниже приведен список наиболее полезных функций: Мощность, модуль, корень и другие.

Имя функции	Тип результата	Описание функции
Abs(x)	совпадает с типом параметра	Модуль в Паскале определяется функцией Abs(x), которая возвращает абсолютное значение (модуль) x. Пример: Если x=6, то Abs(x)=6.
Sqr(x)	совпадает с типом параметра	Вторую силу в Паскале можно вычислить с помощью функции Sqr(x), которая возвращает квадрат x. Пример: Если x=5, то Sqr(5)=25.
Sqrt(x)	Квадратный корень в Паскале можно вычислить с помощью функции Sqrt(x), которая возвращает квадратный корень из x. Например, если x=49, то Sqrt(49)=7. Аргумент функции должен быть положительным числом.
Мощность(x,y)	настоящий	Любая мощность в Pascal вычисляется с помощью Power(x,y). Оно возвращает x в степень y. Например, если основание x=2, а степень y=5, то Power(2,5)=32. В PascalABC мощность можно вычислить с помощью следующей нотации: 2**5 (две звездочки означают умножение).
Int(x)	настоящий	Возвращает целочисленную часть x
Random(x)	Целое число	Возвращает случайное целое число в диапазоне от 0 до x-1
Случайный	настоящий	Возвращает случайное вещественное значение в диапазоне 0…1)
Frac(x)	настоящий	Возвращает дробную часть x
Truncate(x)	x-величина, целое число	Возвращает целочисленную часть x

Задача 3. Вычислите значение y=5x 7-4x 2 +3

Функции в Паскале — мега переменные.

Функции отличаются от процедур тем, что после выполнения функции на ее место в коде ставится число, буква, строка и т.д. Набор встроенных функций Паскаля довольно обширен. Например, чтобы вычислить квадрат числа, можно использовать стандартную функцию sqr(x). Как вы, вероятно, уже поняли, sqr(x) принимает только один вещественный параметр — число.

Внимание. Функции должны быть назначены! Простая запись их как процедур в тексте программы ни к чему не приведет!

Структура функции показана на следующем рисунке.

Если в программу необходимо включить новую уникальную функцию, она должна быть описана так же, как и процедура. О том, как создавать собственные процедуры и функции, вы можете узнать из 10 уроков. Ниже приведена таблица с основными стандартными функциями и процедурами Паскаля.

Операции div и mod.

Иногда нам нужно найти коэффициент или остаток от деления. В таких случаях необходимо использовать такие операции, как div и mod. Обратите внимание, что эти операции выполняются только с целыми числами.

Чтобы найти коэффициент деления, используется оператор div.

25 div 20 = 1;
20 div 25 = 0;
39 div 5 = 7;
158 div 3 = 52.

Mod

Чтобы найти остаток от деления, мы используем оператор mod.

25 mod 20 = 5;
20 mod 25 = 0;
39 mod 5 = 4;
158 mod 3 = 2.

Чтобы окончательно понять, с чем мы имеем дело, решите следующую задачу:

Задача 1: Найдите сумму цифр двузначного числа.

Поскольку эта задача очень проста, мы решим ее с помощью блок-схемы и программы.

program Sumoftwo; var Number, Num1, Num2, Sum: integer; begin write('Введите двузначное число: '); read(Number),<Возьмем число 25>Num1 := число div 10,<25 div 10 = 2>Num2 := число mod 10,<25 mod 10 = 5>Sum := Num1 + Num2,<2 + 5 = 7>write('Сумма двух чисел - ', Sum); end.

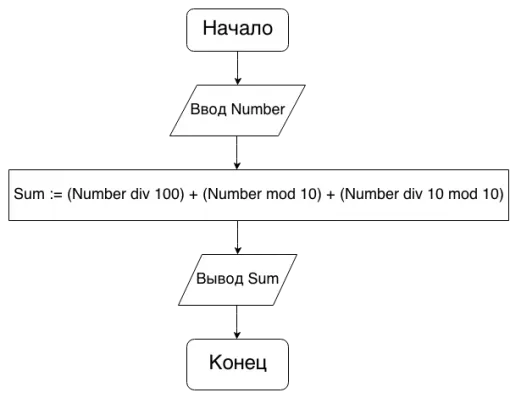
Задание 2: Найдите сумму цифр трехзначного числа.

Несколько более сложная версия предыдущей задачи. Наибольшую трудность представляет вторая цифра.

program Sumoftree; var Number, Sum: integer; begin write('Запишите трехзначное число: '); read(Number),<Возьмем число 255>Сумма := число div 100 + число mod 10 + число div 10 mod 10,<255 div 100 + 255 mod 10 12>write('Сумма трех чисел - ', Sum); end.

И это все. В следующем уроке мы рассмотрим функции PascalABC.Net.

Стандартные арифметические процедуры и функции Pascal

Здесь мы сосредоточимся на некоторых арифметических операциях.

Операция inc в Паскале, произносимая как инкремент, — это стандартная процедура в Паскале, обозначающая увеличение на единицу.

Пример операции inc:

x:=1;инк.(x);пишите.(х)

Более сложное использование процедуры inc: inc(x,n), где x — порядковый тип, а n — целочисленный тип; процедура inc увеличивает x на n.

Пример использования функции odd:

начатьWriteLn(Любопытный(5));WriteLn(Любопытный(4));Конец.

begin WriteLn(Odd(5)); WriteLn(Odd(4)); end.

Пример использования процедуры sqr в Паскале:

varx:Целое число;начатьx:=3;пишите.(sqr(x));Конец.

var x:integer; begin x:=3; writeln(sqr(x)); end .

Формула такая: exp(ln(a)*n), где а — число, n — степень (а>0).

Однако с компилятором Паскаля abc простое умножение намного проще:

WriteLn(мощность(2,3));

Пример использования процедуры sqrt в Паскале:

varx:Целое число;начатьx:=9;пишите.(sqrt(x));Конец.

var x:integer; begin x:=9; writeln(sqrt(x)); end.

Математические операции

В Паскале, как и в большинстве языков программирования, основные математические операции рассматриваются несколько идиосинкразически — например, математические выражения должны записываться в одну строку, а не на нескольких уровнях, как это принято в классической математической нотации. Это достигается за счет более широкого использования скобок, что иногда разочаровывает новичков. Также всегда следует писать символ умножения *. Кроме того, параметры функции всегда должны быть заключены в скобки. Например:

Если компилятор не поддерживает tan.

Базовая арифметика

Имя функции	Оператор	Пример	Примечание
добавить	+	2+2 (=4)
удалить	—	18.3-11 (=7.3)
Умножить	*	7*8 (=56)
Раздел	/	7/8 (=0.875)	Результат всегда реальный
Целочисленная часть деления	div	7 div 2 (=3)
остальная часть дивизии	мод	7 mod 2 (=1)

Все операции сравнения возвращают булево значение, то есть их можно использовать в операторах ветвления и цикла, например.

if 2 + 2 = 4 then writeln (‘Два и два вместе дают четыре!’)

Имя функции	Оператор	Пример
Соответствует	=	2+2=4
Не равны (?)	<>	2+2<>5
Больше, чем	>	72>71.99
Больше или равно	>=	x*x>=0
Менее		0
Меньше или равно		1

Функции для преобразования действительных и целых чисел

Паскаль — это язык программирования со статической сильной типизацией. Это означает, что компилятор не выполняет преобразования значений между типами, что может привести к потере информации. Например, если вы подставите вещественное число в конструкцию, которая возвращает целочисленное значение, компилятор сообщит об ошибке, даже если число является целым. Итак, как мы видели выше, 13 и 11 равны 9, но 13.0 и 11 приведут к сообщению компилятора об ошибке! Чтобы избежать этого, вы должны явно указать преобразование вещественного числа в целое число с помощью следующих функций:

Имя функции	Описание	Пример
Круглый(X)	Возвращает целочисленное значение, наиболее близкое к X	Round(1.7)=2, Round(-3.1)=3
Int(X), Trunc(X)	Возвращает целочисленную часть X	Int(1.8)=1, Trunc(-11.3)=-11
Пол(X)	Возвращает наибольшее целочисленное значение, которое не превышает X	Floor(1.7)=1, Floor(-3.1)=-4
Ceil(X)	Возвращает наименьшее целочисленное значение, которое не меньше X	Ceil(1.7)=2, Ceol(-3.1)=-3

Логические и побитовые операции

Логические операции используются для объединения нескольких логических условий в одно.

Имя функции	Оператор	Пример	Описание
Булевы AND, and, логическое умножение	и	(2+3=5) and (0>-1)	Истинно, если оба оператора истинны
Логическое ИЛИ, или логическое сложение	or	(2+2=5) ή (1=1)	Истинно, если хотя бы один из операторов истинен
Логическое ИЛИ, исключающее ИЛИ	xor	(2+2=5) xor (1=1)	Истинно, если в точности один из операторов истинен.
Отрицательный, логический НЕ, нет	не	не (2+2=5)	Истинно, если один из операторов ложен.

Булевы операторы, применяемые к целочисленным типам, могут использоваться как побитовые операторы. Чтобы получить результат побитовой операции, необходимо представить операнды в двоичном виде (как они представлены в компьютере), а затем применить соответствующую операцию к соответствующим битам, где 1 — истина, 0 — ложь.

13 в бинарной системе становится	1	1	1
11 в двоичном формате становится	1	1	1
9 в двоичном исчислении будет	1	1

Существуют также две другие операции сдвига битов:

Имя функции	Оператор	Пример	Описание
Правый сдвиг	Шр	14 Шр 2 (=3)	Сдвигает двоичные разряды первого оператора вправо на разряды второго оператора; соответствует целочисленной части деления на 2
Левый сдвиг	шл	7 шл 3 (=56)	Сдвигает двоичные биты первого оператора влево на биты второго оператора; соответствует умножению на степень 2.

Алгебраические функции

Серым цветом выделены операции, которые не поддерживаются Turbo Pascal.

Имя функции	Описание	Заменить (для Turbo Pascal)
Pi	Возвращает числовое значение (+3.1415929265353589793238462643383279 … с точностью, заданной текущей формулой)
Abs(X)	Абсолютное значение (модуль) X
Sign(X)	Признак X: 1, если X отрицательный, 1, если X положительный 0, если X = 0
Exp(X)	Экспонента X (e X)
Ln(X)	Натуральный логарифм X
Log2(X)	Логарифм X по основанию 2	Ln(X)/Ln(2)
Log10(X)	Логарифм X по основанию 10	Ln(X)/Ln(10)
LogN(X,Y)	Логарифм Y к основанию X	Ln(Y)/Ln(X)
Мощность(X,Y)	Мощность X Y	Exp(Y*Ln(X))
Sqrt(X)	Квадратный корень из X
Sqr(X)	X-квадрат
Max(X,Y)	Большая часть X и Y
Min(X,Y)	Меньше, чем X и Y

Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы «Инфоурок»).

В настоящее время 54 287 учебных заведений имеют право на накопительную скидку (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

«Креативные инструменты в PowerPoint»

2 слайд Деление целых чисел и остатки В математике деление целых чисел — это деление одного целого числа на другое целое число, где результатом является целая часть результата.

3 Слайд DIV Основные правила — результат деления меньшего числа на большее равен нулю. MOD — результат деления меньшего числа на большее равен меньшему числу. Действие A mod 10 можно использовать для нахождения последней цифры любого целого числа.

4 Слайд Оператор DIV Оператор DIV используется для нахождения целочисленной части деления. Он работает только с целыми числами.

В данном примере n равно 1. Почему? Мы знаем, что DIV ищет целочисленную часть деления, которая в данном примере равна 12 делить на 10, что дает 1,2. Таким образом, целочисленная часть деления равна 1.

5 слайд Оператор MOD Оператор MOD используется для нахождения остатка от деления. Он работает только с целыми числами, не думайте, что это дробь, не запутайтесь!

В данном примере n равно 2. Почему? Мы знаем, что MOD ищет остаток от деления, т.е. в примере 12 делится на 10: значит, остаток от деления равен 2.

Слайд 6 Операторы DIV и MOD Если мы разделим 17 на 3, то получим 5.666666666…. Здесь записано целое число 5, которое является результатом операции DIV. Если мы разделим 17 на 3, то получим 5 как целое число и 2 как остаток. Результатом операции MOD является 2.

7 Слайд Примеры 35 div 10 = 36 div 5 = 77 div 3 = 345 div 10 = 123 div 12 = 44 div 1000 = 11 mod 2 = 32 mod 17 = 18 mod 3 = 1243 mod 100 = 45 mod 100 = 36 mod 10 = 3 7 25 34 10 0 1 1 15 0 43 45 6

8 Слайд Задание 1 Напишите программу, которая определяет количество цифр в последовательности натуральных чисел, делящихся на 6. Программа принимает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда есть число, кратное 6. https://inf-oge.sdamgia.ru/problem?id=120

Заключение

На сегодня это все, думаю, принцип ясен. Если что-то пойдет не так, не ругайте меня — просто напишите в комментариях. В следующей статье мы рассмотрим алгоритмы ветвления. Спасибо вам всем. До свидания =)

В этой статье мы рассмотрим операторы mod и div и их применение в решении задач. Мы рассмотрим несколько примеров с решениями, а также самостоятельно решаемые задачи.

Удачи в программировании.

С помощью mod мы получаем остаток от деления числа a на число b.

Переменная s будет равна 5.

С помощью оператора div мы получим целую часть от деления числа a на число b

Переменная s будет равна 2.

Использование mod при решении задач

Чаще всего оператор mod используется для определения кратности числа и используется в условии (оператор IF)

Задача состоит в том, чтобы определить, является ли число, введенное с клавиатуры, четным.

Чтобы ответить на этот вопрос, разделите число a на mod, деленное на 2 (a mod 2), и сравните это значение с нулем. Условие таково: a mod 2 = 0.

Чтобы узнать, делится ли a на b без остатка, используйте условие:

Также оператор mod используется для определения последней цифры числа

Задание: умножьте последнюю цифру числа на 10 и покажите результат.

Чтобы поместить последнюю цифру числа a в переменную, разделите число на mod на 10. Получим: b:=a mod 10 — последняя цифра числа оказывается в переменной b.

Если мы хотим отделить 2 последние цифры числа, мы делим его на 100; если мы хотим отделить 3 последние цифры, мы делим его на 1000 и так далее.

Чтобы узнать, заканчивается ли a на b, мы должны использовать условное выражение:

Проблема: Если число, введенное с клавиатуры, оканчивается на 5 и делится на 7, печатается «YES», в противном случае печатается «NO».

Используя рассмотренные условия и счетный цикл, мы можем решить следующую задачу:

Подсчитайте количество целых чисел, кратных 9 и оканчивающихся на 5 в диапазоне от 1 до 500.

Использование оператора div при решении задач

Задача: Вам дано трехзначное число. Выясните, является ли оно палиндромным («перевернутым»), т.е. числом, десятичная запись которого читается одинаково слева направо и справа налево.

Выделите первую цифру числа, разделив его на 100.

Отделите последнюю цифру, разделив ее на 10. Вторая цифра не нужна для решения задачи, потому что она не определяет, является ли число палиндромным или нет.

Задания, которые вы должны выполнять самостоятельно:

Дано трехзначное число. Определить:
- является ли сума его цифр двузначным числом
- является ли произведение его цифр трехзначным числом
- больше ли числа a произведение его цифр
- кратна ли пяти сумма его цифр
- кратна ли сумма его цифр числу a
Дано четырехзначное число. Определить:
- равна ли сумма двух первых его цифр сумме двух его последних цифр
- кратна ли трем сума его цифр
- кратно ли четырем произведение его цифр
- кратно ли произведение его цифр числу а

Источник

Оператор div и оператор mod

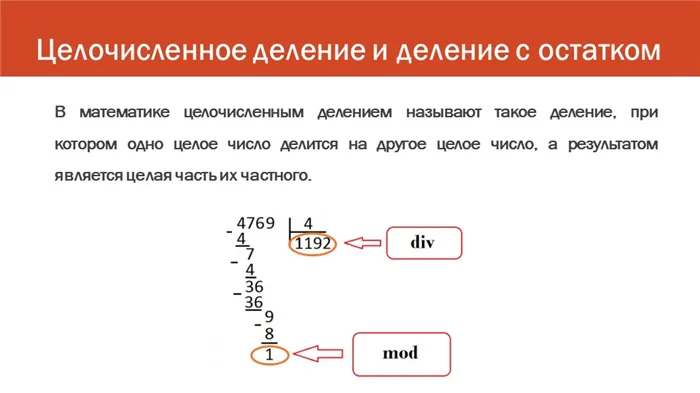
В этой статье речь пойдет о целочисленном делении и делении с остатком.

Итак, что такое целочисленное деление вообще? В математике целочисленным делением называют такое деление, при котором одно целое число делится на другое целое число ,а результатом является целая часть их частного.

То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.

Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e

x — число , которое будем делить на y (делимое)
y — число , на которое будем делить число x (делитель)
z — результат целочисленного деления (целочисленное частное)

Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так

z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!

А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.

x — число , которое будем делить на y (делимое)
y — число , на которое будем делить число x (делитель)
z — остаток

Например (40 / 6) с остатком = 4 с оператором mod будет такой

И как результат получим z=1 .

Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.

Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим

Что такое div и mod в паскале

В чем заключается вопрос: Что такое операции mod и div в языке Pascal. Как с нами работать?

Сложность : легкая .

Постараюсь быть краток, сразу стоит сказать что эти операции работают только с целыми числами, т.е. integer и т.д.
Сначала операция div:
Эта операция используется для того чтобы найти целую часть от деления, как это понять? Допустим у нас есть код:

n у нас будет равно 1. Почему? Как я и сказал div ищет целую часть от деления, т.е. у нас делится 12 на 10, это будет равно 1.2. Целая часть от деления равна 1. Вот это и делает операция div, если допустим 12 div 2, ответ 6.0, целая часть уже равна 6. Т.е. мы как бы делим 12 на 10, но в ответ записывается только целая часть от деления.

Дальше операция mod:
Эта операция уже ищет остаток от деления. Не думайте что это дробная часть, НЕ ПУТАЙТЕ!

Допустим есть код:

Тут остаток от деления равен 2. Другой пример, допустим следующее :

Эти операции в основном используются для того чтобы разбить например трехзначное число на цифры, давайте маленький пример, допустим есть число 123:

Обычно начинают искать с последний цифры, у нас это 3. Чтобы её оторвать надо сделать следующее:

Т.е. мы 123 делим на 10, ответ 12.3 , а остаток равен 3. Первая цифра есть. Дальше 2. Тут делается так, сначала убирается последняя цифра, т.е. 3, с помощью div, а потом с помощью mod ищем 2-ую цифру:

Т.е. сначала у нас из-за div будет 12, а потом с помощью mod у нас появится 2. Ну а последнюю цифру можно найти так:

Вот как то так. Может вы сразу не поймете, но тут надо немного по практиковаться. Удачи! Спасибо за внимание!

Всем привет, как дела? Че делаешь? ммм ясно, понятно. Не будем долго и дружелюбно общаться, проходите, присаживайтесь по удобнее, чувствуйте себя как дома. На улице с каждым днем солнце порабощает планету, мне это нравится, с нетерпением жду прихода молодой теплой, походу грязной и с множеством воды, весны. Но есть и свои плюсы: тепло, птицы, растительность, легкая куртка. А как вы относитесь к весне?
В этой части поговорим о еще двух функциях DIV и MOD, в прошлой части мы говорили об математических операциях, сегодняшние функции тоже по сути ими являются. Поехали =)

DIV, MOD или обычное деление

DIV и MOD похожи на обычное деление, но все таки они для чего то существуют, значит разница быть должна. Вспомним начальную школу и математику, когда вы только-только учились умножать и делить, когда вы еще не подозревали, что судьба вас свяжет с программированием и будете работать «тыж программистом» или же помбуром. Шутки в сторону, так вот вспомним деление «столбиком». Возьмем число 23 и разделим его столбиком, как учили в школе, на число 10.

Вот таким образом мы разделили число 23 на 10. У нас осталась в целой части число 2, а в остатке число 3. Проще говоря наш ответ стал равен двум целым и трем десятых(2.3). Отлично, это было обычное деление, но как будет выглядеть это в случае с MOD и DIV?

MOD — если мы делим число с помощью функции MOD, то в ответ у нас пойдет остаток. По примеру выше, если бы мы делили не обычным делением, а с помощью mod, то ответ у нас был бы 3.

DIV — соответственно наоборот, если мы делим в с помощью DIV то в ответ пойдет только целая часть — 2.

Pascal

Откроем PascalABC и напишем заготовку

Объявим две переменные с целочисленным типом данных

Дальше присвоим переменной «a» какое-либо значение и переменную «b» приравняем к переменной «a».

Отлично, теперь выведем ответ на действие обычного деления на число 100

Теперь проделаем тоже деление, но вместо обычного используем DIV и MOD. Переменную «a» делим с помощью функции DIV, а переменную «b» соответственно функцией MOD и посмотрим что получится.

Как видим, div вывел в ответ целую часть, а mod — остаток.

Разделим число на тысячи, сотни, десятки и единицы

Думаю в голове у многих уже что-то начинает откладываться, давай закрепим знания, напишем не большую программу с линейным алгоритмом, которая будет показывать сколько в число тысяч, сотен, десятков и единиц. Напишем заготовку и объявим две переменные с целочисленным типом данных.

Присвоим переменной «a» числовое значение.

Дальше присвоим переменной «b» действие — деление переменной «a» на число 1000 с помощью функции div.

program chislo;
var
a,b: integer;
begin
a:= 4321;
b:= a div 1000;
a:= a-b*1000;
end.

Теперь напишем команду вывода с новой строки.

Тем самым мы разделили число на тысячи и вывели сколько содержится в нем тысяч, теперь тоже самое проделаем для сотен, десятков и единиц, изменив лишь пару значений и вывод.

И добавим команду вывода в самое начало

program chislo;
var
a,b: integer;
begin
a:= 4321;
writeln( ‘ Число » ‘+a+’ » состоит из’ );
b:= a div 1000;
a:= a-b*1000;
writeln( b+’ тысячи’ );
b:= a div 100;
a:= a-b*100;
writeln( b+’ сотен’ );
b:= a div 10;
a:= a-b*10;
writeln( b+’ десятков’ );
b:= a div 1;
a:= a-b;
writeln( b+’ единиц’ );
end.

Запустим программу и увидим его выполнение

Число «4321» состоит из
4 тысячи
3 сотен
2 десятков
1 единиц

Заключение

Вот и все на сегодня, думаю принцип работы понятен. Если что не так, сильно не ругайте, а пишите в комменты что и как. В следующей статье начнем изучение ветвящихся алгоритмов.
Всем спасибо.
Пока =)

Так как в воскресенье на сайте открывается новая рубрика — решение задач, мы с вами должны по-быстрому изучить основную часть математических операций, функций и процедур.

Давайте разберемся, что такое функция и процедура. Это подпрограмма — часть программы, выполняющая определенный алгоритм и допускающая обращение к ней из различных частей общей программы. В чем же разница между процедурой и функцией?

Процедуры — мини-программы.

Процедуры используются в случаях, когда в подпрограмме необходимо получить несколько результатов. Из картинки, расположенной ниже вы видите, как работает процедура. Входных данных может не быть вовсе, а может быть сто.

Например, программист хочет в своем суперкоде между блоками выходящих значений прописывать 20 амперсандов. Чтобы облегчить себе задачу, он напишет простую подпрограмму.

Функции в Паскале — мега переменные.

Функции отличается от процедуры тем, что после выполнения функции на ее месте в коде ставится одно число, буква, строка и т.д. Набор встроенных функций в языке Паскаль достаточно широк. Например, для того, чтобы подсчитать квадрат числа можно воспользоваться стандартной функцией sqr(x). Как вы, наверное, уже поняли sqr(x) требует лишь один фактический параметр — число.

Обратите внимание! Функции необходимо присваивать! Просто написав их в тексте программы, как процедуры, вы ничего не добьетесь!

Структура функции представлена на картинке ниже.

Если в программу необходимо включить новую уникальную функцию, ее надо описать также, как процедуру. Более подробно о том, как делать собственные процедуры и функции, мы поговорим через 10 уроков. Ниже вы видите таблицу основных стандартных функций и процедур в Паскаль.

Имя Тип аргумента Результат вычисления Пример Abs(x) Целый или Вещ. Модуль х Abs(-6) = 6 Sqrt(x) Вещественный Корень из х Sqrt(25)=5 Sqr(x) Целый и Вещ. Квадрат х Sqr(5)=25 Power(x, a) Вещественный Значение х а Power(5,3)=125 Frac(x) Вещественный Дробная часть х Frac(5.67)=0.67 Sin(x) Вещественный Синус х Sin(45)=0.8509 Cos(x) Вещественный Косинус х Cos(45)=0.5253 Arctan(x) Вещественный Арктангенс х Arctan(5)=1.3734 Int(x) Вещественный Целая часть х Int(5.67)=5.0 Random(x) Целый Случайное число (0..х-1) Random(5)=4 Succ(x) Порядковый Следующий Succ(10)=11 Pred(x) Порядковый Предыдущий Pred(‘Z’)=’Y’ Inc(x, a) Целый X:=X+A Inc(5)=6 Dec(x, a) Целый X:=X-A Dec(25,20)=5 Trunc(x) Вещественный Целая часть х Trunc(5.67)=5 Round(x) Вещественный Округление х до целого Round(5.67)=6 Важно! Если х = 5.5, то результат – 6, а если х = 6.5, то результат тоже 6!?

Очень странная ошибка.

Операции div и mod.

Иногда нам требуется найти частное либо же остаток от деления. В такие моменты на помощь нам приходят такие операции, как div и mod. Заметим, что эти операции выполняются только над целыми числами.

Для того, чтобы найти частное от деления, мы используем операцию div.

25 div 20 = 1;
20 div 25 = 0;
39 div 5 = 7;
158 div 3 = 52.

Для того, чтобы найти остаток от деления, мы используем операцию mod.

25 mod 20 = 5;
20 mod 25 = 0;
39 mod 5 = 4;
158 mod 3 = 2.

Чтобы окончательно понять, с чем мы имеем дело, решим следующую задачу:

Задача 1. Найти сумму цифр двухзначного числа.

Так как эта задача очень простая, мы с вами обойдемся блок-схемой и программой.

Блок-схема

Задача 2. Найти сумму цифр трехзначного числа.

Чуть усложненная версия предыдущей задачи. Самая большая сложность — вторая цифра.

Приоритет div и mod больше, чем приоритете + и -. Поэтому в данной программе можно обойтись без скобок.

Что такое операции mod и div в Pascal?

В чем заключается вопрос: Что такое операции mod и div в языке Pascal. Как с нами работать?

Сложность: легкая.

Постараюсь быть краток, сразу стоит сказать что эти операции работают только с целыми числами, т.е. integer и т.д.

Сначала операция div:

Эта операция используется для того чтобы найти целую часть от деления, как это понять? Допустим у нас есть код:

Дальше операция mod:
Эта операция уже ищет остаток от деления. Не думайте что это дробная часть, НЕ ПУТАЙТЕ!

Источник