Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Теорема
a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r < |b|.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
- 7 * 2 + 1 = 15;
- 2 * 7 + 1 = 15.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Самый удобный способ деления — это столбик.
Попрактикуемся в решении.
Пример
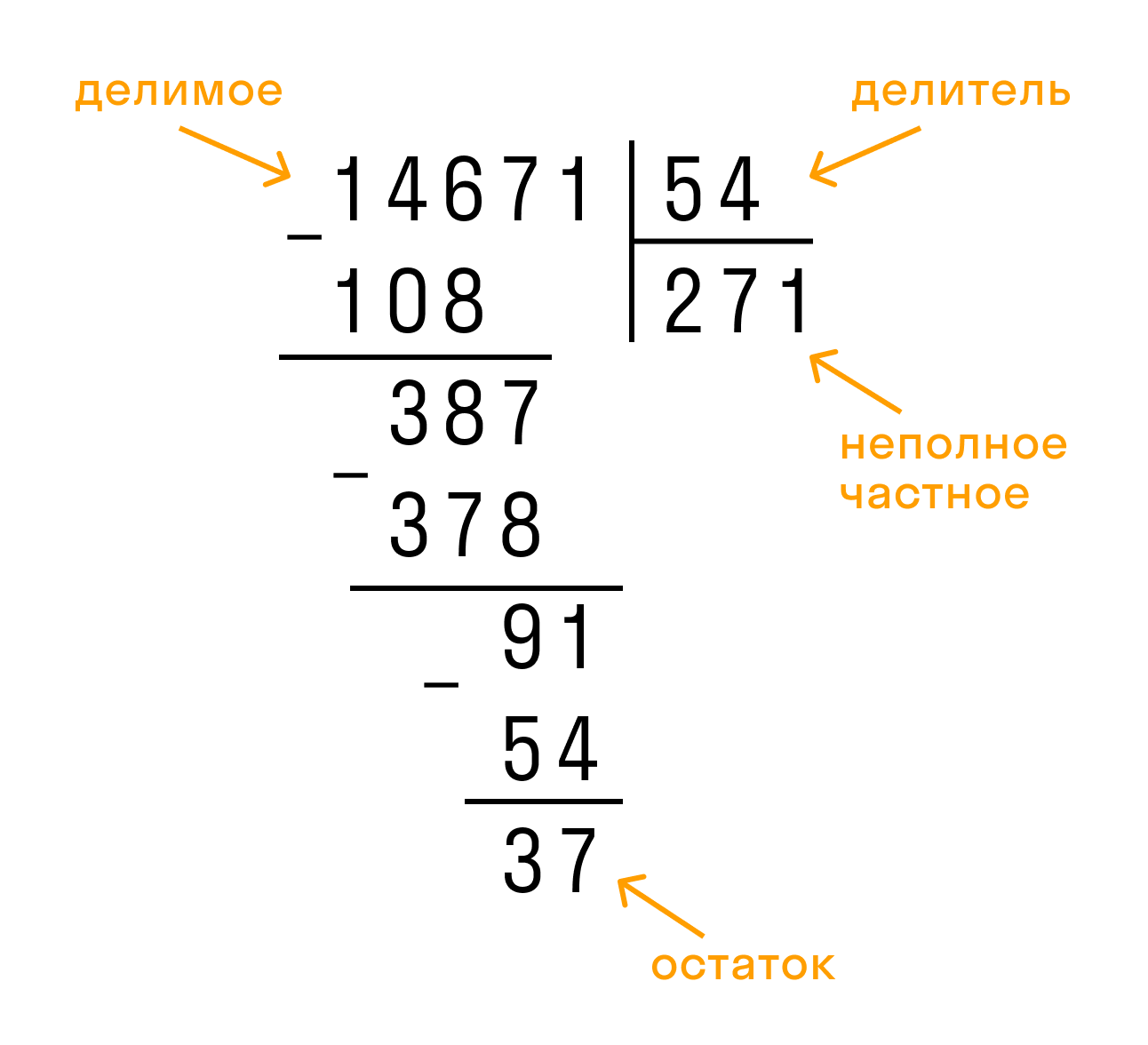
Разделить 14671 на 54.
Как решаем:
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:
r = a − b * q
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Как решаем:
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
r = a − b * q
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Как решаем:
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Автор: Виктор Трофимов, МОУ гимназия №5, г. Волгодонск, Ростовская обл.
В Паскале существует возможность использования трех методов определения кратности числа.
1. С помощью оператора div (целоисчисленное деление). Как это работает?
x := 10 div 2 (переменная x получит значение 5; процессор вычисляет пример 10 / 2 и выдает результат 5)
x := 10 div 3 (переменная x получит значение 3; вычисляется 10 / 3 = 3,33 и отбрасывается дробная часть, такова природа работы оператора div)
x := 10 div 4 (переменная x получит значение 2; 10 / 4 = 2,5 – и опять отбрасывается дробная часть).
2. С помощью оператора mod (остаток от деления).
Тут и понятно, остаток от деления числа, которое полностью делится на делитель, будет равен нулю.
x := 10 mod 2 (переменная x получит значение 0; процессор вычисляет по формуле 10 – ((10 div 2) * 2) = 0, то есть оператор mod возвращает пользователю остаток, который получится в результаты вычитания из делимого числа разницы между первым в сторону уменьшения делящимся нацело на делитель… эмм, надеюсь, понятно. Еще на примерах:
x := 10 mod 3 (переменная x получит значение 1; происходит следующее 10 div 3 = 3 (целое), дальше 10 – 3 (результат) * 3 (делитель) = 1)
x := 10 mod 4 (переменная x получит значение 2; вычисляется 10 – ((10 div 4) * 4)).
Внимательно изучите работу операторов div и mod, они важны для решения задач ГИА по информатике.
3. С помощью функции отбрасывания дробной части числа (не округления, а именно отбрасывания).
trunc(z), где z – вещественное число или математическое выражение.
Примеры:
x := trunc(3.33) (x получит значение 3; «удаляется» дробная часть)
x := trunc(10 / 3) (x получит значение 3, 10 / 3 = 3.33, отбрасываем «,33»)
x := trunc(10 / 2) (x получит значение 5, 10 / 2 = 5 (целое число))
x := trunc(10 / 4) (x получит значение 2, 10 / 4 = 2.5, отбрасываем дробную часть)
Но этот метод не совсем удобен, так как дублирует более понятный в тексте программы div. Таким же образом можно проверить кратность чисел:
Если ((x mod 3) = 0), то число кратно трем (остаток от деления равен нулю).
Если ((x mod 
Как найти цифру, на которую оканчивается число? Все просто, надо найти остаток от деления числа на 10.
Примеры:
Результатом 150 mod 10 будет число 0, т.к. 150 полностью делится на 10. 0 – это последняя цифра числа.
153 mod 10 вернет 3 (153 – ((153 div 10) * 10); 3 – эта цифра, на которую оканчивается число.
87 mod 10 вернет 7 – последнюю цифру числа.
33 mod 10 вернет 3 и т.д. Попробуйте сами: writeln(33 mod 10);
Автор:
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
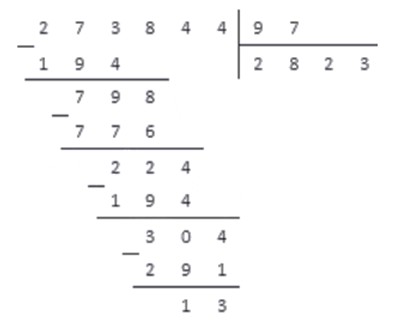
Разделим натуральное число 273844 на натуральное число 97.
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3.
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7-3=4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4-3=1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7÷3=2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Вычислим: 145÷46.
145-46=99.
Число 99 больше, чем 46, поэтому продолжаем последовательное вычитание делителя:
99-46=53.
Повторяем эту операцию еще раз:
53-46=7
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7.
145÷46=3 (остаток 7).
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a<b, то a÷b=0 (остаток a).
Например:
12÷36=0 (остаток 12)47÷88=0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d=a-b·c. Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0, 1, 2, 3 и т.д. Применяя формулу d=a-b·c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b. Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Разделим 267 на 21.
a=267; b=21. Подберем неполное частное.
Используем формулу d=a-b·c и будем последовательно перебирать c, придавая ему значения 0, 1, 2, 3 и т.д.
Если с=0, имеем: d=a-b·c=267-21·0=267. Число 267 больше, чем 21, поэтому продолжаем подстановку.
При с=1 имеем: d=a-b·c=267-21·1=246. Т.к. 246>21, снова повторяем процесс.
При с=2 имеем: d=a-b·c=267-21·2=267-42=225; 225>21.
При с=3 имеем: d=a-b·c=267-21·3=267-63=204; 204>21.
…
При с=12 имеем: d=a-b·c=267-21·12=267-252=15;15<21.
На этом этапе процесс деления можно считать законченным. Неполное частное с=12, а остаток деления равен 15.
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a<b, неполное частное равно нулю, а остаток равен делимомому a. Мы будем рассматривать случай, когда a>b.
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b.
Найти нужно неполное частное c и остаток d.
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a=b·c+d. Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a=b·c+d, тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a=b·c+d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47.
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
3-2=1
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470<899, запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10. В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1, 2, 3.. и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470.
470<899, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47·20=940; 940>899.
Число, которое мы получили на предпоследнем шаге (470=47·10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1-5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1-5, но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899-470=429, 429>47. Повторяем шаги 1-5 алгоритма с числом 429, взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47. Запоминаем разницу — число 1.
2. В записи делимого справа дописываем один нуль. Получаем число 470. Так как 470>429, из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1-1=0. Запоминаем 0.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1, 2, 3 .. и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47·9=423<429, 47·10=470>429. Таким образом, второе искомое слагаемое — 47·9=423.
5. Разность между 429 и 423 равна числу 6. Так как 6<47, это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899=470+423+6. Вспоминаем, что 470=47·10, 423=47·9. Перепишем равенство:
899=47·10+47·9+6
Применим распределительное свойство умножения.
899=47·10+47·9+6=47·(10+9)+6
899=47·19+6.
Таким образом, мы представили делимое в виде уже данной ранее формулы a=b·c+d.
Искомые неизвестные:неполное частное с=19, остаток d=6.
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Разделим числа 42252 и 68.
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800=68·600.
Снова повторяем первые пять шагов алгоритма с числом 1452=42252-40800 и получаем второе слагаемое 1360=68·20
Третий раз проходим шаги аглоритма, но у же с новым числом 92=1452-1360. Третье слагаемое равно 68=68·1. Остаток равен 24=92-68.
В результате получаем:
42252=40800+1360+68+24=68·600+68·20+68·1+24==68·(600+20+1)+24=68·621+24
Неполное частное равно 621, остаток равен 24.
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Проверим, верно ли, что 506÷28=17 (остаток 30).
Сравниваем остаток и делитель: 30>28.
Значит, деление выполнено неверно.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.
Подставляем значения и сравниваем результаты
13·9+5=117+5=122; 121≠122
Значит, в вычисления школьника где-то закралась ошибка.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.
Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.
После подстановки, имеем:
5998=111·54+4=5994+4=5998.
Равенство корректно, а значит, и деление выполнено верно.
Деление c остатком (деление по модулю) — арифметическая операция, играющая большую роль в арифметике, теории чисел и алгебре. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть 






Таким образом, результатами деления с остатком являются два целых числа: 



Примеры.
-
- Проверка:
- Проверка:
-
- Проверка:
- Проверка:
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Содержание
- 1 Определение
- 1.1 Натуральные и целые числа
- 1.2 Обобщения
- 1.2.1 Вещественные числа
- 1.2.2 Гауссовы целые числа
- 1.2.3 Многочлены
- 2 В программировании
- 2.1 Знак остатка
- 2.2 Как запрограммировать, если такой операции нет?
- 3 См. также
- 4 Примечания
- 5 Ссылки
Определение[править | править вики-текст]
Натуральные и целые числа[править | править вики-текст]
Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше.
Для практического выполнения целочисленного деления 




Здесь скобки 
Обобщения[править | править вики-текст]
Вещественные числа[править | править вики-текст]
Если два числа 



Формально:
- если
, то
, где
Пример:
(остаток 1,6)
Гауссовы целые числа[править | править вики-текст]
Гауссово число — это комплексное число вида 



где частное 




Многочлены[править | править вики-текст]
При делении с остатком двух многочленов 

, причём
Пример:
(остаток 3), так как 2x² + 4x + 5 = (x + 1)(2x + 2) + 3
В программировании[править | править вики-текст]
| Язык | Неполное частное |
Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % |
Делимое | |
| Ada | mod | Делитель | |
| rem | Делимое | ||
| ASP | Mod |
Не определено | |
| Бейсик | |
MOD |
Не определено |
| Си (ISO 1990) | / |
% |
Не определено |
| Си (ISO 1999) | / |
% |
Делимое[3] |
| C++ (ISO 2003) | / |
% |
Не определено[4] |
| C++ (ISO 2011) | / |
% |
Делимое[5] |
| C# | / |
% |
Делимое |
| ColdFusion | MOD |
Делимое | |
| Common Lisp | mod |
Делитель | |
rem |
Делимое | ||
| Delphi | div |
mod |
Делимое |
| Eiffel | // |
\ |
Делимое |
| Erlang | div |
rem |
Делимое |
| Euphoria | remainder |
Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() |
MOD() |
Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() |
ОСТАТ() |
|
| FileMaker | Div() |
Mod() |
Делитель |
| Fortran | mod |
Делимое | |
modulo |
Делитель | ||
| GML (Game Maker) | div |
mod |
Делимое |
| Go | / |
% |
Делимое |
| Haskell | div |
mod |
Делитель |
quot |
rem |
Делимое | |
| J | |~ |
Делитель | |
| Java | / |
% |
Делимое[6] |
Math.floorDiv |
Math.floorMod |
Делитель (1.8+) | |
| JavaScript | % |
Делимое | |
| Lua | % |
Делитель | |
| Mathematica | Mod |
Делитель | |
| MATLAB | idivide(?, ?, 'floor') |
mod |
Делитель |
idivide |
rem |
Делимое | |
| MySQL | DIV |
MOD% |
Делимое |
| Objective Caml | mod |
Не определено | |
| Pascal | div |
mod |
Делимое[7] |
| Perl | Нет | % |
Делитель |
| PHP | Нет[8] | % |
Делимое |
| PL/I | mod |
Делитель (ANSI PL/I) | |
| Prolog (ISO 1995) | mod | Делитель | |
| PureBasic | / |
Mod% |
Делимое |
| Python | // |
% |
Делитель |
| QBasic | |
MOD | Делимое |
| R | %% | Делитель | |
| RPG | %REM | Делимое | |
| Ruby | % | Делитель | |
| Scheme | modulo | Делитель | |
| SenseTalk | modulo | Делитель | |
| rem | Делимое | ||
| Tcl | % | Делитель | |
| Verilog (2001) | % | Делимое | |
| VHDL | mod | Делитель | |
| rem | Делимое | ||
| Visual Basic | |
Mod |
Делимое |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получении случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Знак остатка[править | править вики-текст]
Важно отметить, что операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
- Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
- Знак остатка совпадает со знаком делителя: неполное частное округляет к −∞.
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
- Есть сумма n копеек, положительная или отрицательная. Перевести её в рубли и копейки. —
n div 100иn mod 100. Знак остатка совпадает со знаком делимого. - Есть бесконечное клеточное поле, каждая клетка — 16×16 пикселей. В какую клетку попадает точка (x, y), и каковы координаты относительно верхнего левого угла клетки? —
(x div 16, y div 16)и(x mod 16, y mod 16)соответственно. Знак остатка совпадает со знаком делителя.
Как запрограммировать, если такой операции нет?[править | править вики-текст]
Неполное частное можно запрограммировать как ![q = left[frac{a}{b}right]](https://web.archive.org/web/20160430141554im_/https://upload.wikimedia.org/math/f/7/1/f714da379d07864de682eaaf2754b14a.png)
При отсутствии команды mod остаток программируется как 
Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой 
См. также[править | править вики-текст]
- Алгоритм Евклида
- Делимость
- Наибольший общий делитель
- Непрерывная дробь
- Сравнение по модулю
Примечания[править | править вики-текст]
- ↑ Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
- ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
- ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the
/operator is the algebraic quotient with any fractional part discarded. [This is often called “truncation toward zero”.]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится. - ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ N3242=11-0012 (Working draft), текст совпадает с C99
- ↑ К. Арнолд, Дж. Гослинг, Д. Холмс. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
- ↑ Стандарт 1973 года: div — division with truncation.
- ↑ PHP: Arithmetic Operators — Manual
Ссылки[править | править вики-текст]
- Деление с остатком: онлайн-калькулятор
Определение.
Пусть а
— целое
неотрицательное число , а b
— число
натуральное. Разделить а
на b
с остатком — это значит найти такие
целые неотрицательные числа q
и r,
что а=
bq
+ r,
причем r
больше или равно нулю, но меньше b.
Теорема.
Для любого целого
неотрицательного числа а
и натурального
числа b
существуют
целые неотрицательные числа q
и r,
такие что а=
bq
+ r,
причем r
больше или равно нулю, но меньше b.
И эта пара q
и r
единственная для заданных а и b.
Доказательство
существования.
Обозначим через Ь
множество целых неотрицательных чисел,
кратных b
и не
превосходящих
а :
М = {x|x=by,
x
меньше или равен
a}.
Так как для всех
чисел из этого множества выплняется
неравенство х<а+1,
то в множестве М есть наибольше число,
которое обозначим через х0. Это число
имеет вид х0=bq,
причем число b(q+1)
уже не принадлежит множеству М и поэтому
b(q+1)
>a.
Итак, найдено число q
, такое что a
больше или
равно bq,
но меньше bq+b.
Из этих неравенств следует, что a—bq
больше или равно 0, но меньше b.
Если обозначить a—bq
через r
, то имеем a—bq
=r,
т.е. r
+bq
=a
и r
больше или равно нулю .Это означает, что
q-
неполное частное, а r
— остаток при делении.
Доказательство
единственности.
Предположим, что
а=
bq
+ r,
где r
больше или равно нулю, но меньше b
и а=
bq1
+ r1,
r1
больше или равно нулю, но меньше b,
причем, например, r>
r1
. Тогда имеем bq
+ r=bq1
+ r1,
r—r1=
bq1
—bq=b(q1
-q).
Поскольку 0 меньше или равен r1<r<
b,
то r—r1<b
. Но
с другой стороны r—r1=b(q1
-q),и
потому делится на b.
Это противоречие
и доказывает, что другой пары чисел с
требуемыми свойствами не существует.
.3.Методика
изучения деления с остатком в начальной
школе.
В начальных классах
обычно рассматриваются те случаи,
которые сводятся к табличному делению.
Особенностью деления с остатком
является то,
что находятся два числа (частное и
остаток). Сначала надо раскрыть конкретный
смысл действия деления с остатком (по
решать задачи, пр: 10 яблок – 3 девочки;
сделать наглядную интерпретацию).
Далее следует раскрыть отношение м/у
делителем и остатком (если при делении
получается остаток, то он всегда будет
меньше делителя). Для этого нужно по
решать примеры на деление последовательных
чисел на 2, на 3 и т.д. пр: 10:2=5, 11:2=5 ост.1,
12:2=6, 13:2=6 ост.1, 14:2=7 (здесь будет только
один остаток – 1(единица)); 9:3=3, 10:3=3 ост.1,
11:3=3 ост.2, 12:3=4 (при делении на 3 будет
всегда только 2 остатка – 1 или 2).
При раскрытии
общего смысла сначала лучше брать пары
примеров, один на деление с остатком,
другой – без остатка, пр:16:5, 15:5
(пример-помощник), а потом можно брать
примеры без примера-помощника.
При делении с
остатком рассуждаем так: пр: 37:8, 37 на 8
не делится. Самое большое число,
которое делится без остатка на 8 – 32,
32:8=4, из 37 вычитаем 32, получаем остаток
– 5. Следовательно, при делении 37 на 8
получаем 4 с ост.5.
Билеьт 4. 1.
Древнерусское государство
Христианство пришло
на Русь, в кот уже существовали
воспитательные идеалы: общинные ценности,
этнический характер, языческие
представления Главные воспитатели –
семья и община, а воспитательные средства
– участие в труде семьи и общины. С
принятием христианства было положено
книжное просвещение. Независимость от
Византии, кот князь Владимир поставил
непременным условием принятия
христианства, государственная
самостоятельность – все это предопределило
особый путь развития на его просвещение
(несмотря на безусловное влияние визант
культуры). С укреплением гос-ва на Руси
возникает потребность в грамотных
людях. В Киеве князь Владимир открывает
«школы учения книжного», куда повелевает
отдавать детей дворцовой знати. Главным
носителем просвещения на Руси, как и во
всем средневековом мире, было духовное
сословие. Греческое духовенство сразу
после крещения Руси привнесло византийские
культурные традиции. Постепенно
воспитывается и собственное духовенство.
В отличии от Зап Европы, в организации
церковных школ для мирян с целью
подготовки будущих священников не было
нужды, т к священнические места
передавались от отца к сыну. Это до 17 в.
Определило характер воспитания как
семейный и домашний. Домашний порядок
сущ-л и в обучении. Приходское обучение
велось на дому у свящ-ка или дьякона,
было бесплатным и всесословным. Содержание
обучения составляло: 1)чтение книг Свящ.
Писания и дух. Содержания 2)обучение
письму и счету 3)до монголо-татарск
нашествия греч духовенство учило
риторике, философии, греч яз Знания
белого духовенства на первых порах было
ограничено: основы вероучения и
грамотность. Наиболее образованными
людьми в Древней Руси были представители
монашества. Монашеский образ жизни и
мел большое влияние: аскетическая
жизнь давала пример победы духа над
житейской приземленностью, корыстолюбием
и страстями, дух
труды монахов сочетались с владениями
навыка чтения и письма,
монахи изучали труды Отцов Церкви,
богословов, философов, занимались
переводом греч книг, писали
летописи и составляли сборники
нравоучений, несли обширное соц служение.
Просвещение на Руси особенно широко
распространилось в период правления
Ярослава Мудрого (1019-1054): огромные
киевские храмы становились центрами
просвещения, создавались библиотеки и
разворачивалась переводческая
деятельность, князь заботился о
поставлении в священники грамотных
людей, был принят новый свод законов
-Ярославский устав, в кот присутствовал
в христ духе брачный кодекс, исключалось
принуждение при вступлении в брак,
многоженство, повышалась ответственность
родителей за детей, школы возникают не
только при великокняжеском дворе, но и
при дворах князей Переславля, Владимира.
Чернигова, Ростова, Турова и др городах,
в Киеве строились многочисленные
монастыри. Особенно возросло значение
Киево-Печ монастыря, кот стал центром
книжного знания, летописания и обучени,
в общественном сознании возрастает
уважение к книжному человеку, умеющему
не просто читать, но и толковать дух
лит-ру, обладающему дух мудростью, в
Киево-Печ м-ре переписывались и изучались
греч книги и составлялись оригинальные
произведения, в кот осмысливалось
своеобразие развития Руси как православного
гос-ва. Развитие его культуры как
продолжение культуры Византии и христ
Рима. Именно в Киево-Печ м-ре начал свою
деятельность митр. Илларион, автор
«Слова о законе и благодати», в кот он
показал эту преемственность Руси с
христ миром. Сравнивал князя Владимира
с апп. Петром и Павлом. Вторым крупным
ценром просвещения был Вел Новгород. В
1960-х годов под рук Янина было найдено
большое количество берестяных грамот
– свидетельство о широком распространении
грамотности среди разных слоев населения
(учились чтению, счету, письму, навыкам
ремесла и торговли). Известно соборное
поучение новг еп Иоанна – изложение
свода правил о повседневном поведении.
Наставления такого плана восходили к
поучениям греч отцов 4в., как важный
способ педагогич воздействия Церкви
на мирян и духовенство. Кроме Киева и
Новгорода стали возвышаться Владимир,
Суздаль, Ростов. Известно наставление
детям киевского князя Константина
Всеволодовича (12в.) – наказ опекуну
княжеских детей о необходимости найти
для детй доброго дух наставника. Т.о.
главное условие доброй жизни для детей
было наличие перед глазами воспитателя
высокого образца мыслей и дел. Очень
важна была роль духовников. Их насталения
были даже более действенными, чем
родительские, т.к. за ними сотял авторитет
Церкви. Т.о.
в связи с особенностями общественного
развития и Церк устроения Древн Руси:
не возникло
массовой потребности в общественной
школе 1)стремление к обучению удовлетворялось
в частном порядке и велось дома у
священников, на приходах, в монастырях,
в процессе чтения дух книг, окормления
у духовников.2)Обучение мирян и духовенства
было примерно одинаковым по содержанию.
Включало вероучение, грамоту, счет,
письмо, церк пение 3)В больших городах
(торговых и ремесленных центрах)
создавались училища. При архиерейских
домах учили греч яз, риторике, диалектике
– тривиум. 4)При несовершенстве
средневекового учения оно отличалось
целостностью, стройностью идеалов,
системностью, доступностью. 5)Рус
просвещение всецело осоновывалось на
истине Свящ Писания, а само учение
представлялось дух возрастанием человека
через просвещение его ума и сердца
светом христианства. 6)В правосл культуре
дух возрастание всегда шло под рук-ом
Ц. Исходя из этого и Др Рус просвещение
носило искл-но церковн хар-р. 7)Письменные
источники о воспитании в Др Руси:
Произведения фолклора, Былинный эпос,
основывающ-ся на христ идеалах, Жития
святых, Летописи, сказания
2.Понятие
«величина». Термин
«величина» вначале появился в философской
литературе. Scalar – число. Скалярные
величины характеризуются только числовым
значением. Существуют разные подходы
к понятию скалярной величины, наиболее
распространенный из них – аксиоматический.
Пусть имеется непустое множество М,
состоящее из элементов любой природы,
на котором задано бинарное отношение
«меньше» и определена операция сложения.
Тогда это множество называется системой
однородных положительных скалярных
величин, а его элементы – однородными
положительными скалярными величинами,
если выполняются следующие аксиомы:
А1. ¥
a,
b
€ М:
а=b,
a<b, b<a.т
A2. ¥ a,
b, c € M:
a<b
и b<c =>
a<c
(транзитивность отношения «меньше»).
A3. ¥
a,
b
€ М:
Э!
(существует
единственно) c
€ M:
c = a+b
(однозначность суммы).
А4. ¥ a,
b € М:
a+b = b+a
(коммутативность сложения). A5. ¥ a,
b, c € M:
a + (b+c) = (a+b) + c
(ассоциативность сложения). А6. ¥ a,
b € М:
а < a+b
(монотонность сложения). A7. ¥ a,
b € M:
a<b,
Э! c
€ M
: b = a+c
(возможность вычитания). А8. ¥ a
€ М,
¥ n
€ N,
Э! b
€ M:
a = n*b
(возможность умножения). A9.
¥ a,
b
€ М,
Э
n
€ N:
a<nb
(аксиома
Архимеда).
|
А10. |
{ai} |
a1<a2<…<an<… |
|
{bj} |
b1<b2<…<bm<… |
(Пусть дана
последовательность {ai}
(а
ите) элементов множества М,
которая обладает свойством a1<a2<….<an<…
и последовательность {bj}
(b
жите),
обладающая свойством b1<b2<….<bm<…;
причем ai
< bj
для любых i и j. Тогда существует
единственный элемент c
€ M
такой, что an<c<bm).В
основе измерения величин лежит один
принцип: измеряемый объект сравнивается
с эталоном, то есть с предметом или
явлением, величина которого принята за
единицу измерения. В результате сравнения
получается число, характеризующее
измеряемую величину. Пусть дана
величина a
€ M,
которую нужно измерить и эталон, единица
измерения c
€ M.
Тогда мерой величины а
при единице измерения е
называется такое положительное
действительное число х,
что а = х*е.
При этом х
называют числовым значением величины
а.
Пишут: me (a) =
x. Системой
измерения положительных скалярных
величин называется отображение множества
М
в множество положительных действительных
чисел R+
(f: M→R+), согласно которому каждой величине
ставится в соответствие положительное
действительное число. Это отображение
удовлетворяет следующим условиям: В
множестве М
существует величина е,
мера которой равна единице. Э е € М;
m(е) = 1 (существование единицы измерения).
1)Инвариантность меры: равные величины
имеют равные меры. 2)
¥ a, b € М;
a = b => me(a) = me(b).3)Аддитивность
меры.
Если величина
равна сумме нескольких величин, то ее
мера равна сумме мер слагаемых. В процессе
измерения величин необходимо различать:
1.Объект или явление, к которому относится
величина. 2.Саму величину как свойство
объекта или явления. 3.Числовое значение
величины. Для каждого рода величин
существует несколько стандартных единиц
измерения. Различают основные и
производные единицы величины. В СССР
1-го января 1963 года была введена
международная система единиц (СЕ). В ней
основными единицами являются: для длины
– метр, для времени – секунда, для массы
– килограмм. Аксиоматический подход
неприемлем в НШ. В практике преподавания
в НШ используются следующие свойства
положительных скалярных величин:
Скалярные величины могут быть однородными
и разнородными. Однородными называются
величины, выражающие одно и то же свойство
объектов или явлений, Любые две величины
одного рода сравнимы, Величины одного
рода можно складывать и вычитать, в
результате получается величина того
же рода. Если обе величины выражены в
одних и тех же единицах, то сложение и
вычитание величин сводится к соответствующим
операциям над их числовыми значениями.
Сложение разнородных величин не имеет
смысла, Величину можно умножать на
положительное число и нуль. В результате
получается величина того же рода, Если
числовые значения величин me(a) = x, mе(b) =
y, то отношение xy называют отношением
величины а к b.
Некоторые разнородные
величины умножают и делят, в результате
получаются величины третьего рода, В
курсе математики НШ рассматриваются
следующие виды величин: Геометрические
величины (длина отрезка, площадь плоской
фигуры, объем тела), Масса. Время. Задача:
Основание одного прямоугольника – 6
см., а высота на 2 см меньше; основание
второго прямоугольника – 2 см, а высота
– в три раза больше. Во сколько раз
площадь первого прямоугольника больше
площади второго? Какие операции над
величинами выполняются в процессе
решения задачи? — вычитание из длины
равной 6 см длины равной 2 см. — умножение
величины на натуральное число. — умножение
величин (длины на длину), в результате
получается площадь. — деление площади
на площадь. В результате получается
положительное действительное число.
Различные свойства объектов и явлений
окружающего мира взаимосвязаны. Эти
связи выражаются в определенных
зависимостях между соответствующими
величинами. Применение математических
методов позволяет выражать зависимости
между величинами в виде формул. Рассмотрим
тройку величин, связанных с равномерным
прямолинейным движением: u, t, s. S = v*t.
Исследуем эту формулу. Для этого положим
в формуле u = k, где k – некое постоянное
число. Тогда, подставляя это значение
в формулу, получим: S = k*t. Отсюда зависимость
между расстоянием и временем прямо
пропорциональная. Положим t = k = const t. S =
k*v. Зависимость между S и u также
прямо-пропорциональна.
S – k; k –
const S; k = vt или
v = kt. Зависимость
между скоростью и временем
обратно-пропорциональна. Знание этих
зависимостей помогает решать текстовые
задачи различной сложности. Задача1:
За два часа велосипедист проехал 30 км.
Какой путь проделает велосипедист за
оставшиеся 6 часов, если будет двигаться
с той же скоростью? 1 способ: 6:2 = 3; 30*3 = 90
Основан на прямо-пропорциональном
соотношении между временем и расстоянием.
2 способ: 302 = 15; 15*6 = 90 Основан на основной
формуле. Задача
2: Скорый
поезд, двигаясь со скоростью 80 кмчас,
проходит расстояние между a и b за 3 часа.
За какое время можно проехать это
расстояние на электричке, если она идет
со скоростью 40 кмчас. 1 способ: 80:40 = 2;
3*2 = 6 Основан на обратно-пропорциональной
зависимости между скоростью и расстоянием.
2 способ: 80*3 = 240;
240:40 = 6; Основан на основном правиле.
Аналогичные зависимости существуют
между другими тройками величин: 1) Цена,
стоимость, количество. Задача:
Из 80 м ткани сшили 10 одинаковых
пододеяльников. Сколько наволочек можно
было сшить из этой ткани, если на каждую
наволочку расходуется в 4 раза меньше
ткани, чем на пододеяльник. 1 способ:
8010 = 8; 84 = 2; 80/2 = 40. Основан на расходе на
одну наволочку и формуле. 2 способ: 10*4 =
40. На обратно-пропорциональной зависимости
между расходом и количеством. 2) Работа
(A), время (t), производительность(k). A =
k*t. Встречаются и другие зависимости
между величинами. 3) Стальной брусок
Объемом 60 см3 имеет массу 468 гр. Какова
масса стального бруска объемом 25 см3?
Зависимость между массой и объемом: m =
k*v; k – масса одного см3. 1 способ: 468 60
*25 = 195 гр. Основано на основной формуле.
2 способ: 60 : 25 = 2,4; 468 : 2,4 = 195. На прямой
пропорциональности между массой и
объемом. 4) Для перевозки груза нужно 15
трехтонных машин. Сколько потребуется
для этого же груза пятитонных машин? 3
величины: грузоподъемность машин,
количество машин, масса груза. 1 способ:
15*3 = 45; 455 = 9. По формуле. 2 способ: 5:3 = 53;
15 : 53 = 9. Основан на обратной пропорциональности
между количеством и грузоподъемностью.
3
Величины в методике. Понятие
величины (В,) широко применяется не
только в математике, но и в других науках.
В естественных науках под величинами
понимают определенные свойства физических
тел и некоторые из величин(объем, масса,
время, скорость, цены) изучают в курсе
математики начальной школы. В математике
теория величин строится с помощью
исходных свойств, характеризующих
величины. Например, в первом классе
отрезки сравнивают сначала с помощью
наложения. Это приводит к пониманию
длины. Два отрезка имеют одну и ту же
длину, если один совпадает с другим при
наложении, если же какой-то из сравниваемых
отрезков при наложении накладывается
только на часть другого, не покрывая
его целиком, то говорят, что второй
отрезок длиннее первого. В ходе такой
практической работы дети обнаруживают
свойство длины отрезков, устанавливается
отношение прядка. Общими для введения
понятия величины являются следующие
этапы: 1)Задается некоторое множество
А, которое является областью определений
величины. 2. из данного рода величин
выбирается нужная величина (е), которая
называется единицей измерения.
3. Осуществляется процесс измерения.
Данная величина сравнивается с выбранной
единицей измерения. Результатом чего
является некоторое значение величины.
Изучение величин в начальном курсе
математики имеет прикладной характер:
учащиеся учатся определять длины
отрезков, массу тел, время по часам, дату
по календарю и т. п. Ученики, оканчивающие
начальную школу, должны знать, что на
множестве изученных величин определены
отношения равенства и неравенства и
эти отношения устанавливаются как
практически, так и косвенно. Все величины
можно измерить, причем для каждой есть
свой способ измерения, сущность которого
заключается в сравнении данного объекта
с единицей его измерения. Величины
одного и того же рода можно складывать,
вычитать, а также умножать и делить на
отвлеченные числа, можно находить часть
от величины. Между величинами одного и
того же рода существует определенная
зависимость. Её необходимо знать для
преобразования величин. Обучение
измерению различных величин строится
по одной схеме: дети сравнивают величины
на глаз, вводится единица измерения
величины и устанавливается отношение
между ними и ранее рассмотренными,
величины преобразуются, величины
сравниваются путем измерения, учащиеся
производят операции над величинами,
Величины не выделяется как особая тема
и изучаются с другими темами; могут
иллюстрировать арифметические темы, а
геометрический материал может служить
средством наглядности при изучении
величин и их измерений, Обучение
учащихся измерению длины. С
любыми объектами, для которых можно
установить отношения длиннее, короче,
шире, уже учащиеся знакомятся до
поступления в школу. В первом классе
эти отношения уточняются, расширяется
множество объектов к которым они могут
быть отнесены.Сначала сравнивают объекты
на глаз, затем — путем наложения.
Накладывают выбранную единицу измерения
на объект. Единицы измерения могут быть
разными. Чтобы не было разных результатов,
детям сообщают , что существует единая
единица измерения – сантиметр. Учитель
должен обратить внимание на то, что не
все предметы можно сравнивать путем
наложения. Их нужно измерить одной и
той же меркой, а полученные числа
сравнить. Вводятся стандартные единицы
измерения. Сантиметр = изготовляют
модель. Измерять ей трудно, линейкой с
делениями удобней. Линейка – первая
счетная машин. Измерительные навыки
учащихся закрепляют при решении простых
задач на увеличение или уменьшение на
несколько единиц, сравнение длин
отрезков. Понятие дм формируется на
основе уже знакомого понятия см. Учащиеся
должны убедиться, что легче большие
предмеды измерять с помощью дм, а не см.
Они учатся измерять в см и дм, преобразовывать
см в дм. Можно изготовить модель дм, а
также модель- мерку , длиной в 10дм и
поработать с ней на занятиях, посвященных
метру. Вводится отношение 1 м=10дм=100см.
Учащиеся преобразуют 327см=3м2дм7см=3м27см.
Вводится мм. Учащиеся чертят в тетрадях
1см, на глаз делят на 10 частей-1/10см.
Вводится отношение1см=10мм. На изучение
1 км возможна экскурсия на местность.
На последнем этапе составляется всводная
таблица. 1км=1000м, 1м=10дм, 1дм=10см, 1см=10мм,
1м=100см, 1дм=100см. таким образом понятие
длины отрезка формируется в процессе
математической деятельности детей.
Собирается эмпирический материал,
обрабатывается, возникает потребность
в измерении длины. Обучение
учащихся измерению массы Многие
предметы тяжелее, легче, одинаковы.
Сравнивая на глаз можно ошибиться. Таким
способом обосновывается использование
весов. Сначала рычажные весы, кг и гр
–показывает гиря, циферблатные весы –
отклонение на 1 деление — 1гр. Возможна
экскурсия в магазин, на рынок, если
брольшие массы – на предприятие. В конце
– таблица: 1т=1000кг,1ц=100кг, 1т=10ц,1кг =100гр.
Обучение
учащихся измерению площади Подготовка
– с первых уроков. Сравнивают площади
наложением , выполняют упражнения, в
которых следует установить, из скольких
треугольников, квадратов и прямоугольников
состоит фигура. Затем учитель показывает,
как измерит площадь с помощью палетки.
До этого вводится единица площади –
1см2.
Можно в тетради начертить квадрат со
стороной в 1см, потом в см2
измеряется площадь прямоугольников и
квадратов. Потом – палетка: сколько
полных сколько неполных, складываем.
Затем знакомимся с формулами. Также по
палетке можно показать соотнесение
1дм2=10см2.
можно изготовить модель квадратного
метра. В конце – таблица:1м2=100дм2,
1м2=10000см2,1дм2=100см2.
Обучение
учащихся измерению времени В
начальной школе учитель обобщает знания
детей о понятиях: старше/моложе,
раньше/позже, вчера/сегодня. Устанавливаются
отношения между мерами времени.
Составляются задачи на нахождение
конца, начала и продолжительности
события. В качестве наглядности можно
использовать: Песочные часы, Цифровые
часы, Календарь, Координатный луч, Нужно
научить ребенка называть время по часам.
Учитель должен объяснить устройство
(назначение стрелок).Вводится понятия
часов, минут, затем суток, календарь:
число, месяц в году, число дней в месяце,
недель в году и т.д.Затем – век ( о
долгожителях /деревья, люди, животные/).
Луч – исчисление времени от РХ. Таблица:
1ч=60мин. 1мин.=60сек. 1век=100лет.
Билет 6.
Педколлесктив
Специфической
особенностью педагогического коллектива
является его преимущественно женский
состав, что не может не влиять на характер
взаимоотношений, возникающих в нем.
Женские коллективы более эмоциональны,
более подвержены смене настроений,
более конфликтны. Однако нужно иметь в
виду, что в то же время женщины по своей
природе более предрасположены к
воспитательной деятельности, более
гибки в выборе приемов и способов
педагогического воздействия. Необходимое
представительство обоих полов в
педагогическом коллективе обеспечивает
его гармоничность и целостность.
Недостаток мужского представительства
в школе должен быть компенсирован за
счет привлечения родителей-отцов к
воспитательной деятельности во внеурочное
время. Неотъемлемой функцией пед.
коллектива является педагогизация
окружающей среды – формирование
педагогической культуры его членов.
Еще одна особенность состоит в высокой
степени самоупровляемости.
При
социально-психологическом анализе
коллектива выделяют формальную
(официальную) и неформальную (неофициальную)
организационные структуры.
Формальная
структура коллектива
обусловлена официальным разделением
труда, правами и обязанностями его
членов. Каждый учитель находится в
официальных, деловых отношениях с
коллегами, руководителями школы.
Отношения между учителями и администрацией
школы — директором и завучами —
регламентируются должностными
инструкциями и распоряжениями.
Неформальная
организационная структура
педагогического коллектива возникает
на основе действительных, а не только
предписанных функций. Неформальная
структура коллектива представляет
собой сеть реально сложившихся отношений
между его членами. Такие отношения
возникают на основе симпатий и антипатий,
уважения, любви, доверия или недоверия,
желания или нежелания сотрудничества.
Такая структура отражает внутреннее,
порой скрытое, незримое состояние
коллектива.
В современной
психолого-педагогической литературе
отмечается, что настроение и эмоциональный
тонус, уровень взаимоотношений в
коллективе определяются сложившимся
в нем социально-психологическим климатом.
По аналогии с климатом географическим
благоприятный социально-психологический
климат означает, что человеку в коллективе
с таким климатом более уютно, комфортно,
здесь он может проявить себя в
профессиональном отношении.
Называют следующие
основные функции социально-психологического
климата:
консолидирующая
— заключается в сплочении членов
коллектива, в объединении коллективных
усилий на решение учебно-воспита- тельных
задач;
стимулирующая —
состоит в создании «эмоциональных
потенциалов» коллектива, его жизненной
энергии, которая затем реализуется в
педагогической деятельности;
стабилизирующая
— обеспечивает устойчивость внутриколлектив-
ных отношений, создает необходимые
предпосылки для успешного вхождения в
коллектив новых педагогов;
регулирующая —
проявляется в утверждении норм
взаимоотношений. В психологии выделяют
основные показатели положительного
социально-психологического климата:
— удовлетворенность
членов коллектива своим пребыванием в
коллективе, процессом и результатами
труда;
-признание
авторитета руководителей, совмещающих
признаки формальных и неформальных
лидеров;
высокая степень
участия членов коллектива в управлении
и самоуправлении коллективом;
организованность
членов коллектива, дисциплина;
продуктивность
работы;
практическое
отсутствие текучести кадров.
К числу факторов,
препятствующих формированию положительного
психологического климата в коллективе,
относятся конфликты — резкое обострение
противоречий, возникающих в сфере
непосредственного общения людей.
В педагогическом
коллективе выделяют три основные группы
конфликтов. Первая группа — профессиональные
конфликты. Они возникают как реакция
на препятствия к достижению целей
профес- сионально-педагогической
деятельности. Вторая группа — конфликты
ожиданий, возникают в тех случаях, когда
поведение педагога не соответствует
нормам взаимоотношений, принятым в
педагогическом коллективе. Третья
группа — конфликты личностной
несовместимости.
Методическая
работа в школе
Профессиональная
подготовка учителя не заканчивается в
стенах педагогического учебного
заведения, она продолжается на протяжении
всего периода профессиональной
деятельности.
В соответствии с
планами повышения квалификации учителей
один раз в пять лет они проходят
специальное обучение на курсах повышения
квалификации. Кроме того, в каждой школе
существует специально организованная
система методической работы, которая
призвана совершенствовать научно-методическую
подготовку учителей. В общем виде задачи
методической работы можно сформулировать
следующим образом:
систематическое
изучение, обобщение и распространение
педагогического опыта и внедрение
достижений педагогической науки;
повышение уровня
предметной подготовки учителей;
организация работы
по изучению новых образовательных
программ, учебных планов, образовательных
государственных стандартов;
овладение новыми
формами и методами обучения и воспитания;
организация работы
по изучению новых нормативных документов
и инструктивно-методических материалов;
оказание
научно-методической помощи учителям;
Повышение общего
уровня профессионально-педагогической
культуры.
В большинстве школ
создаются координационные органы
методической работы —
методические советы
Наиболее
распространенной формой методической
работы в школе является
предметное методическое объединение
учителей.
Эффективной формой
методической работы является проведение
единого
методического дня
(например, один раз в четверть). По мере
необходимости может быть организована
и такая форма методической работы как
школа молодого учитея. Одной
из коллективных форм методической
работы в школе является
деятельность педагогического коллектива
по избранной научно-методической теме.
Профессиональный
рост учителя
Для выполнения
своих сложных педагогических обязанностей
учитель должен обладать
профессиональной пригодностью,
то есть комплексом способностей,
нравственных, физических, нервно-психических
качеств. Это, прежде всего, любовь к
детям. Также педагог должен обладать
коммуникабельностью, наблюдательностью,
тактичностью, развитым воображением,
организаторскими способностями и
высокой требовательностью к себе.
В современной
психолого-педагогической литературе
выделяют следующие уровни в профессиональном
росте учителя:
Педагогическая
умелость.
Это обстоятельное
знание своего учебного предмета, владение
психолого-педагогической теорией,
системой учебно-воспитательных умений
и навыков.
Педагогическое
мастерство — это
уровень совершенного владения
педагогической деятельностью. Это
«отшлифованность» методов и приемов
применения психолого-педагогической
теории на практике. Основой мастерства
являются прежде всего фундаментальные
знания и выработанные на их основе
умения, выступающие в тесном единении
с личностными качествами учителя и его
способностями к творчеству.
Педагогическое
творчество.
Оно выражается во
внесении в учебно-воспитательную
деятельность каких-либо методических
усовершенствований. Творчество —
появление чего-то нового. К условиям,
стимулирующим творческий процесс, можно
отнести: создание особого микроклимата
в педагогических коллективах,
ориентированного на доброжелательность,
взаимоподдержку, взаимообучение;
альтернативность, вариативность и
разумную свободу
в педагогической
деятельности; самообразование; оказание
необходимой научно-методической помощи
и др.
4. Педагогическое
новаторство. Это высший уровень
профессионализма учителя. Оно включает
в себя внесение и реализацию существенно
новых, прогрессивные теоретических
идей, принципов и методов в процессе
обучения и воспитания. Новаторство —
прогрессивные нововведения, совершенствующие
практику, а не отрицание существующей
теории и практики с некоторой относительной
новизной.










 , то
, то  , где
, где 
 (остаток 1,6)
(остаток 1,6)

 , причём
, причём 
 (остаток 3), так как
(остаток 3), так как